题目内容
已知向量
=（2
sin
，2），
=（cos，cos2），设f（x）=
，
（I）求f（x）的最大值及取得最大值时x的集合．
（II）当f（x）=2时，求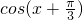
的值．
解：（I）f（x）==2sincos+2cos2=sin
+cos+1=2sin（+
）+1，
故当 （+ ）=2kπ+
时，即 x=4kπ+
，k∈z时，f（x）取最大值 为 3，
此时，x的集合为{x|x=4kπ+，k∈z }．
（II）当f（x）=2时，sin（+ ）=
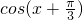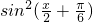，∴=1-2
=1-2×
=，
故所求的式子的值等于．
分析：（I） 利用两个向量的数量积公式和二倍角公式 化简f（x）的解析式，由（+ ）=2kπ+，解出函数取最大值时x的集合，最大值为3．
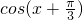（II）当f（x）=2时，sin（+ ）=，由=1-2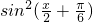求出它的值．
点评：本题考查两个向量的数量积公式的应用，二倍角公式的应用，以及函数取最值的条件，化简f（x）的解析式是解题的突破口．
=2sincos+2cos2=sin+cos+1=2sin（+ ）+1，故当 （
+ ）=2kπ+ 时，即 x=4kπ+，k∈z时，f（x）取最大值 为 3，此时，x的集合为{x|x=4kπ+
，k∈z }．（II）当f（x）=2时，sin（
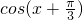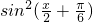+ ）=，∴=1-2=1-2×=，故所求的式子的值等于
．分析：（I） 利用两个向量的数量积公式和二倍角公式 化简f（x）的解析式，由（
+ ）=2kπ+，解出函数取最大值时x的集合，最大值为3．（II）当f（x）=2时，sin（
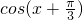+ ）=，由=1-2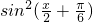求出它的值．点评：本题考查两个向量的数量积公式的应用，二倍角公式的应用，以及函数取最值的条件，化简f（x）的解析式是解题的突破口．
练习册系列答案
相关题目
=0与圆(x-cosβ)2+(y+sinβ)2=
的位置关系是 
=0与圆(x-cosβ)2+(y+sinβ)2=
=（2sinωx，cos2ωx），向量
=（cosωx，
），其中ω＞0，函数f（x）=
•
，若f（x）图象的相邻两对称轴间的距离为π．
，恒有|f（x）-m|＜2成立，求实数m的取值范围．
＝(2cosα,2sinα), 
＝(3cosβ,3sinβ),若
与圆
的位置关系是( )