Question

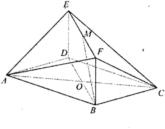已知菱形ABCD与矩形BDEF所在平面互相垂直，且BD=2BF，若M为EF的中点，BD∩AC=O
（I）求证：BM∥平面AEC；
（II）求证：平面AEC⊥平面AFC；
（III）若AF与平面BDEF成60°角，求二面角A-EF-C的余弦值．

Answer 1

分析：（I）先由EM平行且等于BO?四边形EOBM为平行四边形?EO∥BM?BM∥平面AEC．
（II）先利用条件推出OF⊥OE和AC⊥平面BDEF．合在一起可推得OF⊥平面AEC，就可推得结论成立．
（III）先找到∠AMC为二面角A-EF-C的一个平面角，然后在△AMC中求出∠AMC的余弦值即可．

解答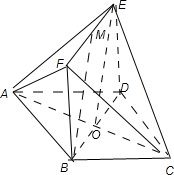：解；（I）证明：连接EO∵EM平行且等于BO
四边形EOBM为平行四边形，
∴EO∥BM又EO?平面AEC，BM?平面AEC
∴BM∥平面AEC．

（II）证明：连接OF，不妨设BD=2BF=2，则OE=OF=

2

，
∴OE²+OF²=EF²．∴OF⊥OE
∵AC⊥BD，平面ABCD⊥平面BDEF且交于BD
∴AC⊥平面BDEF，又∵OF?BDEF?AC⊥OF
∵OE∩AC=0，OE，AC?平面AEC，
∴OF⊥平面AEC∵OF?平面AFC
∴平面AEC⊥平面AFC．

（III）∵AO⊥平面BDEF，∴∠AFO为AF与平面BDEF所成的角，即∠AFO=60°．
不妨设BD=2BF=2，则OE=OF=

2

，∴OA=

6，

AD=

7

．
∴AF=AE=CE=CF=2

2

．连接AM，CM，∵AM⊥EF，CM⊥EF．
∴∠AMC为二面角A-EF-C的一个平面角．
在△AMC，AM=CM=

7

，AC=2

6

，
∴cos∠AMC=-

5

7

．
∴二面角A-EF-C的余弦值为-

5

7

．

点评：本题综合考查了线面平行和面面垂直的证明以及二面角的求法．是道综合性极强的好题．在证明线面平行时，其常用方法是在平面内找已知直线平行的直线．当然也可以用面面平行来推导线面平行．