Question

已知函数f（x）=ln（e^x+a）（a为常数）是实数集R上的奇函数，函数g（x）=λf（x）+sin x是区间[-1，1]上的减函数．
（1）求a的值及λ的范围．
（2）讨论关于x的方程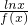=x²-2ex+m的根的个数．

Answer 1

解：（1）∵f（x）是在R上的奇函数，∴f（0）=0，∴ln（1+a）=0，∴a=0．
∵g（x）在[-1，1]上单调递减，
∴x∈[-1，1]时，g′（x）=λ+cos x≤0恒成立
∴λ≤-1，
（2）由（1）知f（x）=x，∴方程为=x²-2ex+m，
令f₁（x）=，f₂（x）=x²-2ex+m，
∵f′₁（x）=
当x∈（0，e）时，f′₁（x）＞0，∴f₁（x）在（0，e]上为增函数；
当x∈（e，+∞）时，f′₁（x）＜0，∴f₁（x）在（e，+∞）上为减函数；
∴当x=e时，[f₁（x）]_max=f₁（e）=．
而f₂（x）=（x-e）²+m-e²
∴当m-e²＞时，即m＞e²+时方程无解．
当m-e²=时，即m=e²+时方程有一解．
当m-e²＜时，即m＜e²+时方程有两解．
分析：（1）利用f（x）是在R上的奇函数，求出a的值，利用g（x）在[-1，1]上单调递减，则导数小于等于0，由此可求λ的范围．
（2）构造函数，求出函数的最值，比较最值之间的关系，即可得到结论．
点评：本题考查导数知识的运用，考查函数的单调性，考查函数的最值，考查分类讨论的数学思想，属于中档题．