题目内容
已知方程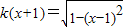 有两个不相等的实数解,则k的范围是( )
有两个不相等的实数解,则k的范围是( )A.k≥
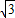
B.0<k≤
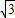
C.0≤k<
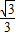
D.0<k<
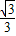
【答案】分析:先将方程 有两个不相等的实数解转化为直线y=k(x+1)与(x-1)2+y2=1(y≥0)有两个不同交点时求k的范围,然后结合直线与圆的相交的性质可求出k的范围.
有两个不相等的实数解转化为直线y=k(x+1)与(x-1)2+y2=1(y≥0)有两个不同交点时求k的范围,然后结合直线与圆的相交的性质可求出k的范围.
解答: 解:方程
解:方程 有两个不相等的实数解等价于
有两个不相等的实数解等价于
y=k(x+1)与 有两个不同交点
有两个不同交点
即y=k(x+1)与(x-1)2+y2=1(y≥0)有两个不同交点,如图示
当直线y=k(x+1)与(x-1)2+y2=1(y≥0)相切时圆心到直线的距离为: =1,求得k=
=1,求得k=
∴0≤k<
故选C.
点评:本题主要考查直线与圆的相交的基本性质.直线与圆的方程是高考的重点也是一个重要考点,其基本性质要熟练掌握并能灵活运用.
 有两个不相等的实数解转化为直线y=k(x+1)与(x-1)2+y2=1(y≥0)有两个不同交点时求k的范围,然后结合直线与圆的相交的性质可求出k的范围.
有两个不相等的实数解转化为直线y=k(x+1)与(x-1)2+y2=1(y≥0)有两个不同交点时求k的范围,然后结合直线与圆的相交的性质可求出k的范围.解答:
 解:方程
解:方程 有两个不相等的实数解等价于
有两个不相等的实数解等价于y=k(x+1)与
 有两个不同交点
有两个不同交点即y=k(x+1)与(x-1)2+y2=1(y≥0)有两个不同交点,如图示
当直线y=k(x+1)与(x-1)2+y2=1(y≥0)相切时圆心到直线的距离为:
 =1,求得k=
=1,求得k=
∴0≤k<

故选C.
点评:本题主要考查直线与圆的相交的基本性质.直线与圆的方程是高考的重点也是一个重要考点,其基本性质要熟练掌握并能灵活运用.

练习册系列答案
相关题目

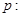 方程
方程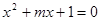 有两个不相等的负实根;
有两个不相等的负实根;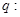 不等式
不等式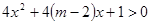 的解集为
的解集为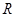 .若“
.若“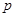 ∨
∨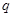 ”为真命题,“
”为真命题,“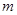 的取值范围.
的取值范围.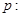 方程
方程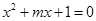 有两个不相等的负实根;
有两个不相等的负实根;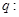 方程
方程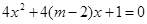 无实根,若"
无实根,若"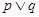 "为真,"
"为真,"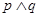 "为假,求
"为假,求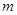 的取值范围。
的取值范围。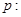 方程
方程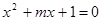 有两个不相等的负实根,
有两个不相等的负实根,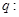 方程
方程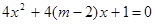 无实数根,若“
无实数根,若“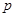 或
或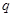 ”为真,“
”为真,“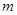 的取值范围。
的取值范围。