题目内容
如图，四边形ABCD是菱形，∠ABC=60°，PB⊥平面ABCD，MA∥PB，PB＝AB＝2MA．
（Ⅰ）证明：AC∥平面PMD。
（Ⅱ）求直线BD与平面PCD所成的角的正弦值；
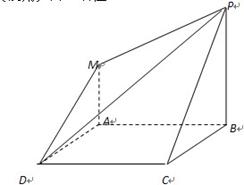
（Ⅰ）解:取DC的中点E，以A为原点，AE所在的直线为x轴、AB所在的直线为y轴，AM所在的直线为z轴建立坐标系，┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈2分
则A(0,0,0), B(0,1,0), C(
,
,0), D(,–,0), M(0,0,), P(0,1,1) ┈┈4分
∴
=(,,0), 
=(,–,–) 
=(0,1, )
∴=+，又AC
平面PMD，∴AC∥平面PMD┈┈┈┈┈┈┈┈┈┈┈6分
（Ⅱ）
=（0，–1，0），
=(–,,1)
设
⊥平面PCD，则=（1，0，），
=（，–
，0）┈┈┈┈┈┈┈┈9分
设直线BD与平面PCD所成的角为
，
则sin=
=
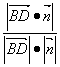.┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈12分
练习册系列答案
相关题目
如图，四边形ABCD与A′ABB′都是边长为a的正方形，点E是A′A的中点，A′A⊥平面ABCD．
如图，四边形ABCD为正方形，QA⊥平面ABCD，PD∥QA，QA=AB=
如图，四边形ABCD为矩形，且AD=2，AB=1，PA⊥平面ABCD，PA=1，E为BC的中点．
如图，四边形ABCD内接于⊙O，如果它的一个外角∠DCE=64°，那么∠BOD
如图，四边形ABCD为正方形，PD⊥平面ABCD，PD∥QA，QA=AB=