题目内容
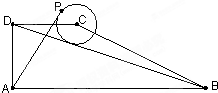如图；在直角梯形ABCD中，AB⊥AD，AD=DC=2，AB=6，动点P在以点C为圆心且与直线BD相切的圆上运动，设| AP |
| AD |
| AB |
[1，
]
| 5 |
| 3 |
[1，
]
．| 5 |
| 3 |
分析：建立直角坐标系，写出点的坐标，求出BD的方程，求出圆的方程；设出P的坐标，求出三个向量的坐标，将P的坐标用m，n表示，代入圆内方程求出范围．
解答：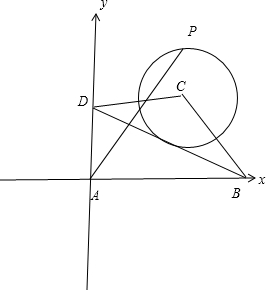
解：以A为坐标原点，AB为x轴，DA为y轴建立平面直角坐标系，则A（0，0），D（0，2），C（2，2），B（6，0）
直线BD的方程为x+3y-6=0，C到BD的距离d=
=
∴以点C为圆心，且与直线BD相切的圆方程为（x-2）2+（y-2）2=
，
设P（x，y）则
=（x，y），
=（0，2），
=（6，0）
∴（x，y）=（6n，2m）
∴x=6n，y=2m，
∵P在圆内或圆上
∴（6n-1）2+（2m-1）2≤
，
解得1≤m+n≤
．
故答案为：[1，
]．
解：以A为坐标原点，AB为x轴，DA为y轴建立平面直角坐标系，则A（0，0），D（0，2），C（2，2），B（6，0）直线BD的方程为x+3y-6=0，C到BD的距离d=
| 2 | ||
|
| ||
| 5 |
∴以点C为圆心，且与直线BD相切的圆方程为（x-2）2+（y-2）2=
| 2 |
| 5 |
设P（x，y）则
| AP |
| AD |
| AB |
∴（x，y）=（6n，2m）
∴x=6n，y=2m，
∵P在圆内或圆上
∴（6n-1）2+（2m-1）2≤
| 2 |
| 5 |
解得1≤m+n≤
| 5 |
| 3 |
故答案为：[1，
| 5 |
| 3 |
点评：通过建立直角坐标系将问题代数化、考查直线与圆相切的条件、考查向量的坐标公式．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
如图，在直角梯形ABCD中，∠A=∠D=90°，AB＜CD，SD⊥平面ABCD，AB=AD=a，SD=
如图，在直角梯形ABCP中，BC∥AP，AB⊥BC，CD⊥AP，AD=DC=PD=2．点E、F分别是PC、BD的中点，现将△PDC沿CD折起，使PD⊥平面ABCD，
如图，在直角梯形ABCD中，AB∥CD，AD=CD=1，AB=3，动点P在BCD内运动（含边界），设
如图，在直角梯形ABCD中，已知BC∥AD，AB⊥AD，AB=4，BC=2，AD=4，若P为CD的中点，则