题目内容
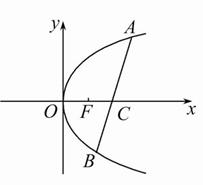
在平面直角坐标系xOy中,过定点C(p,0)作直线与抛物线y2![]() =2px(p>0)相交于A,B两点,如图,设动点A(x1,y1)、B(x2,y2).
=2px(p>0)相交于A,B两点,如图,设动点A(x1,y1)、B(x2,y2).
(1)求证:y1y2为定值;
(2)若点D是点C关于坐标原点O的对称点,求△ADB面积的最小值;
(3)是否存在平行于y轴的定直线l,使得l被以AC为直径的圆截得的弦长恒为定值?若存在,求出l的方程;若不存在,请说明理由.
1)当直线AB垂直于x轴时,
y1=![]() p,y2=-
p,y2=-![]() p,
p,
因此y1y2=-2p2(定值);
当直线AB不垂直于x轴时,设直线AB的方程为
y=k(x-p),
由![]() 得ky2-2py-2p2k=0,
得ky2-2py-2p2k=0,
∴y1y2=-2p2.
因此有y1y2=-2p2为定值.
(2)∵C(p,0),∴D(-p,0),∴|DC|=2p.
S△ADB=![]() |DC|·|y1-y2|.
|DC|·|y1-y2|.
当直线AB垂直于x轴时,
S△ADB=![]() ·2p·2
·2p·2![]() p=2
p=2![]() p2;
p2;
当直线AB不垂直于x轴时,由(1)知y1+y2=![]() ,
,
因此|y1-y2|=![]()
=![]() >2
>2![]() p,
p,
∴S△ADB>2![]() p2.
p2.
综上,△ADB面积的最小值为2![]() p2.
p2.
(3)假设存在直线l:x=a满足条件.
设AC中点E(![]() ,
,![]() ),|AC|=
),|AC|=![]() ,
,
因此以AC为直径的圆的半径r=![]() |AC|
|AC|
=![]()
![]() =
=![]()
![]() ,
,
AC中点E到直线x=a的距离d=|![]() -a|,
-a|,
∴所截弦长为:
2![]() =2
=2![]()
=![]()
=![]() ,
,
当p-2a=0,a=![]() 时,
时,
弦长=![]() =p为定值.
=p为定值.
这时直线l的方程x=![]() .
.

练习册系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是