题目内容
(本小题满分12分)已知椭圆 (
( )的离心率为
)的离心率为 ,且经过点
,且经过点 .
.
(1)求椭圆的标准方程;
(2)设 关于
关于 轴的对称点为
轴的对称点为 ,已知
,已知 为椭圆的上顶点,直线
为椭圆的上顶点,直线 ,
, 分别交
分别交 轴于点
轴于点 ,
, ,求
,求 的值.
的值.
(1) .(2)
.(2)
【解析】
试题分析:(1)依题意得 又
又 即
即 ①
①
将 代入椭圆方程得
代入椭圆方程得 ②联立①②解得
②联立①②解得 .
.
(2) 与
与 关于
关于 轴对称,得
轴对称,得 ,又
,又 ,得到直线
,得到直线 方程为
方程为 ,
,
直线 方程为
方程为 ,令
,令 ,可得
,可得  ,
, ,计算得
,计算得 .
.
试题解析:(1)依题意得
又 ①
①
因为 在椭圆上,
在椭圆上,  ② 2分
② 2分
联立①②解得
 椭圆方程为
椭圆方程为 . 5分
. 5分
(2) 与
与 关于
关于 轴对称,
轴对称, ,
,
 为椭圆上顶点
为椭圆上顶点
 7分
7分
 直线
直线 方程为
方程为 ,令
,令 ,
, 9分
9分
 直线
直线 方程为
方程为 令
令 ,
, 11分
11分
即 12分
12分
考点:1.椭圆标准方程及其几何性质;2.直线方程;3.直线与椭圆的位置关系.
考点分析: 考点1:椭圆的标准方程 考点2:椭圆的几何性质 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
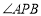 的平分线,
的平分线, 是下半圆的中点.求证:直线PC经过点
是下半圆的中点.求证:直线PC经过点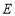 .
.
 ”,则输出的
”,则输出的 ( )
( )
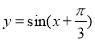 的图象,可将函数
的图象,可将函数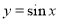 的图象向左平移
的图象向左平移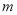 个单位长度,或向右平移
个单位长度,或向右平移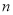 个单位长度(
个单位长度(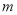 ,
,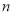 均为正整数),则
均为正整数),则 的最小值是( )
的最小值是( )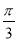 B.
B.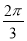 C.
C.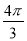 D.
D.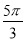
 ,则
,则 的是( )
的是( ) B.
B. C.
C. D.
D.
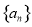 是等差数列,若
是等差数列,若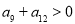 ,
,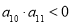 ,且数列
,且数列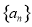 的前
的前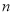 项和
项和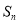 有最大值,那么当
有最大值,那么当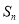 取得最大值时,
取得最大值时,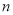 等于 .
等于 . 在
在 上的图象是( )
上的图象是( )
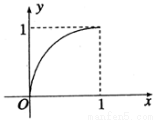
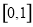 上的函数
上的函数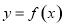 的图象如图所示,对于满足
的图象如图所示,对于满足 的任意
的任意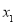 ,
,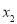 ,给出下列结论:
,给出下列结论: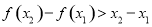 ;
;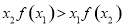 ;
;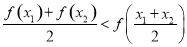 ;
;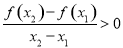 .
.
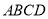 中,
中,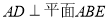 ,
,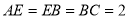 ,
,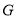 是
是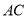 中点,
中点,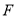 为
为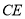 上的点,且
上的点,且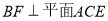 .
.
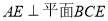 ;
;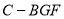 的体积.
的体积.