题目内容
已知x,y满足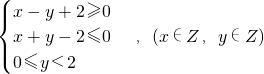 ,每一对整数(x,y)对应平面上一个点,则过这些点中的其中3个点可作不同的圆的个数为
,每一对整数(x,y)对应平面上一个点,则过这些点中的其中3个点可作不同的圆的个数为
- A.45
- B.36
- C.30
- D.27
B
分析:画出可行域,找出可行域中的整数点,利用组合数求出所有的取三点的方法,再减去共直线不能共圆的,和四点共圆的重复情况即可.
解答: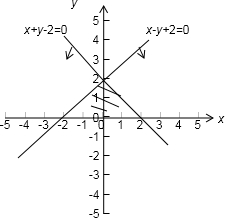 解:作出不等式组
解:作出不等式组 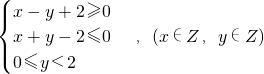 可行域
可行域
可行域中所有的整数点有(-2,0); (-1,0)(-1,1);(0,0);(0,1);(1,0);(1,1);(2,0)
经过其中任意不共线的三点作直线可作不同的圆,则可作不同的圆的个数是:C83-C53-C33=45.
再减去其中四点共圆的情况:
(-1,0)(-1,1);(0,0);(0,1);
和(0,0);(0,1);(1,0);(1,1)
和(-1,0)(-1,1);(1,0);(1,1)
共3C43-3=9种情况
∴符合题意的情况共有45-9=36.
故选B.
点评:求完成某事件的方法数常用的方法是排列、组合的方法有时还用列举的方法.
分析:画出可行域,找出可行域中的整数点,利用组合数求出所有的取三点的方法,再减去共直线不能共圆的,和四点共圆的重复情况即可.
解答:
 解:作出不等式组
解:作出不等式组 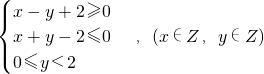 可行域
可行域可行域中所有的整数点有(-2,0); (-1,0)(-1,1);(0,0);(0,1);(1,0);(1,1);(2,0)
经过其中任意不共线的三点作直线可作不同的圆,则可作不同的圆的个数是:C83-C53-C33=45.
再减去其中四点共圆的情况:
(-1,0)(-1,1);(0,0);(0,1);
和(0,0);(0,1);(1,0);(1,1)
和(-1,0)(-1,1);(1,0);(1,1)
共3C43-3=9种情况
∴符合题意的情况共有45-9=36.
故选B.
点评:求完成某事件的方法数常用的方法是排列、组合的方法有时还用列举的方法.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
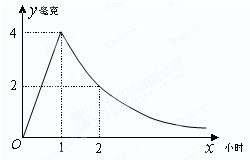 病人按规定的剂量服用某药物,测得服药后,每毫升血液中含药量y=Max(毫克)与时间y=Max(小时)满足:前1小时内成正比例递增,1小时后按指数型函数y=Max(M,a为常数)衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.
病人按规定的剂量服用某药物,测得服药后,每毫升血液中含药量y=Max(毫克)与时间y=Max(小时)满足:前1小时内成正比例递增,1小时后按指数型函数y=Max(M,a为常数)衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.