题目内容
已知tanα是方程x2+2xsecα+1=0的两个根中较小的根,求α的值.
解:∵tanα是方程x2+2xsecα+1=0的较小根,
∴方程的较大根是cotα.
∵tanα+cotα=-2secα,即
∴ .
.
解得 ,或
,或 .
.
当 时,tanα=
时,tanα= ,cotα=
,cotα= ;
;
当 时,tanα=
时,tanα= ,cotα=
,cotα= ,不合题意.
,不合题意.
∴ .
.
分析:由方程的两根之积为1和较小根为tanα得到方程较大的根为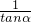 即cotα,然后根据两根之和等于-2secα列出等式,利用同角三角函数间的基本关系化简得到sinα的值,根据正弦函数的周期和特殊角的三角函数值求出α的值,代入到两根之中检验得到符合题意的值.
即cotα,然后根据两根之和等于-2secα列出等式,利用同角三角函数间的基本关系化简得到sinα的值,根据正弦函数的周期和特殊角的三角函数值求出α的值,代入到两根之中检验得到符合题意的值.
点评:本题要求学生利用韦达定理解决数学问题,同时要求学生灵活运用同角三角函数间的基本关系化简求值,学生容易忽视对α值的检验.
∴方程的较大根是cotα.
∵tanα+cotα=-2secα,即

∴
 .
.解得
 ,或
,或 .
.当
 时,tanα=
时,tanα= ,cotα=
,cotα= ;
;当
 时,tanα=
时,tanα= ,cotα=
,cotα= ,不合题意.
,不合题意.∴
 .
.分析:由方程的两根之积为1和较小根为tanα得到方程较大的根为
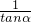 即cotα,然后根据两根之和等于-2secα列出等式,利用同角三角函数间的基本关系化简得到sinα的值,根据正弦函数的周期和特殊角的三角函数值求出α的值,代入到两根之中检验得到符合题意的值.
即cotα,然后根据两根之和等于-2secα列出等式,利用同角三角函数间的基本关系化简得到sinα的值,根据正弦函数的周期和特殊角的三角函数值求出α的值,代入到两根之中检验得到符合题意的值.点评:本题要求学生利用韦达定理解决数学问题,同时要求学生灵活运用同角三角函数间的基本关系化简求值,学生容易忽视对α值的检验.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 的值;
的值; ,
, 的值.
的值.