题目内容
集合A={1,2,3,a},B={3,a2},则使A∪B=A成立的a的个数是( )
| A.2个 | B.3个 | C.4个 | D.5个 |
∵A∪B=A成立,∴B⊆A.
由集合元素的互异性可知:a2≠3,a2=1,2,a,解得a=±1,±
,0.
再由集合元素的互异性可知:a≠1.
①当a=-1时,A={1,2,3,-1},B={3,1},满足B⊆A;
②当a=
时,A={1,2,3,
},B={3,2},满足B⊆A;
③当a=-
时,A={1,2,3,-
},B={3,2},满足B⊆A;
④当a=0时,A={1,2,3,0},B={3,0},满足B⊆A.
综上可知:使A∪B=A成立的a的个数是4.
故选C.
由集合元素的互异性可知:a2≠3,a2=1,2,a,解得a=±1,±
| 2 |
再由集合元素的互异性可知:a≠1.
①当a=-1时,A={1,2,3,-1},B={3,1},满足B⊆A;
②当a=
| 2 |
| 2 |
③当a=-
| 2 |
| 2 |
④当a=0时,A={1,2,3,0},B={3,0},满足B⊆A.
综上可知:使A∪B=A成立的a的个数是4.
故选C.

练习册系列答案
相关题目
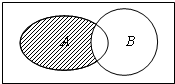 (2012•汕头一模)已知全集U=R,集合A={1,2,3,4,5},B=[2,+∞),则图中阴影部分所表示的集合为( )
(2012•汕头一模)已知全集U=R,集合A={1,2,3,4,5},B=[2,+∞),则图中阴影部分所表示的集合为( )