题目内容
设定函数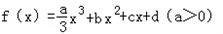
，且方程f′（x）-9x=0的两个根分别为1，4．
（Ⅰ）当a=3且曲线y=f（x）过原点时，求f（x）的解析式；
（Ⅱ）若f（x）在（﹣∞，+∞）无极值点，求a的取值范围．
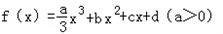，且方程f′（x）-9x=0的两个根分别为1，4．（Ⅰ）当a=3且曲线y=f（x）过原点时，求f（x）的解析式；
（Ⅱ）若f（x）在（﹣∞，+∞）无极值点，求a的取值范围．
解：由得f′（x）=ax2+2bx+c
因为f′（x）﹣9x=ax2+2bx+c﹣9x=0的两个根分别为1，4，
所以
（*）
（Ⅰ）当a=3时，又由
（*）式得 解得b=﹣3，c=12
又因为曲线y=f（x）过原点，所以d=0 故f（x）=x3﹣3x2+12x
（Ⅱ）由于a＞0，所以“
在（﹣∞，+∞）内无极值点”
等价于“f′（x）=ax2+2bx+c≥0在（﹣∞，+∞）内恒成立”．
由（*）式得2b=9﹣5a，c=4a．
又△=（2b）2﹣4ac=9（a﹣1）（a﹣9）
解
得a∈[1，9]
即a的取值范围[1，9]
因为f′（x）﹣9x=ax2+2bx+c﹣9x=0的两个根分别为1，4，
所以
（*）（Ⅰ）当a=3时，又由
（*）式得 解得b=﹣3，c=12 又因为曲线y=f（x）过原点，所以d=0 故f（x）=x3﹣3x2+12x
（Ⅱ）由于a＞0，所以“
在（﹣∞，+∞）内无极值点”等价于“f′（x）=ax2+2bx+c≥0在（﹣∞，+∞）内恒成立”．
由（*）式得2b=9﹣5a，c=4a．
又△=（2b）2﹣4ac=9（a﹣1）（a﹣9）
解
得a∈[1，9] 即a的取值范围[1，9]
练习册系列答案
阅读快车系列答案
相关题目
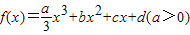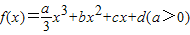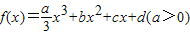，且方程f′（x）-9x=0的两个根分别为1，4．
，且方程f′（x）-9x=0的两个根分别为1，4．
，且方程f′（x）-9x=0的两个根分别为1，4．
，且方程f′（x）-9x=0的两个根分别为1，4．
，且方程f′（x）-9x=0的两个根分别为1，4．