题目内容
一个圆锥经过轴的截面（称为轴截面）是边长为2的等边三角形，则该圆锥的体积是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、3π |
分析：根据题意算出底面半径r=1，利用正三角形的性质算出圆锥的高h=
，利用圆锥的体积公式加以计算，可得答案．
| 3 |
解答：解：根据题意，可得
∵圆锥的轴截面是边长为2的正三角形，
∴底面半径r=1，高h=
r=
，
可得圆锥的体积是V=
πr2h=
π
故选：B
∵圆锥的轴截面是边长为2的正三角形，
∴底面半径r=1，高h=
| 3 |
| 3 |
可得圆锥的体积是V=
| 1 |
| 3 |
| ||
| 3 |
故选：B
点评：本题给出轴截面是正三角形的圆锥，求它的体积．考查了等边三角形的性质和圆锥的体积公式等知识，属于基础题．
练习册系列答案
相关题目
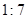；④平行圆锥轴的截面是一个等腰三角形．
的图像是以直线
为轴，以坐标轴为渐近线的等轴双曲线，记作C．
（2） 
的图像是以直线
为轴，以坐标轴为渐近线的等轴双曲线，记作C．
