题目内容
 是
是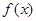
 的导函数,满足
的导函数,满足 ,若
,若 则下列正确的是( )
则下列正确的是( )
A. | B. | C. | D. |
A
解析试题分析:∵f(x)是定义在R上的可导函数,∴可以令f(x)= ,∴f′(x)=
,∴f′(x)= ,∵f′(x)>f(x),ex>0,∴f′(x)>0,∴f(x)为增函数,∵正数a>0,∴f(a)>f(0),∴
,∵f′(x)>f(x),ex>0,∴f′(x)>0,∴f(x)为增函数,∵正数a>0,∴f(a)>f(0),∴ 即
即 ,故选A.
,故选A.
考点:本题考查了利用导数研究函数单调性
点评:此类问题常常要根据已知选项构造特殊函数,然后利用导数法研究函数的单调性,从而利用单调性比较大小,是一道好题

练习册系列答案
相关题目
设函数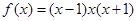 ,则满足
,则满足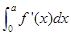 =0的实数a的有( )
=0的实数a的有( )
| A.3个 | B.2个 | C.1个 | D.0个 |
计算定积分 的值是( )
的值是( )
A.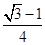 | B.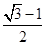 | C.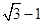 | D.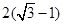 |
已知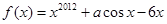 ,且
,且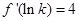 ,则
,则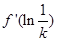 =( )
=( )
| A.-4 | B.4 | C.8 | D.-16 |
若函数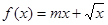 在区间
在区间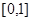 单调递增,则m的取值范围为
单调递增,则m的取值范围为
A.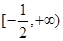 | B.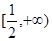 | C.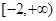 | D.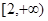 |
 在
在 处可导,
处可导, 为常数,则
为常数,则 ( )
( )
A. | B. | C. | D.0 |
在曲线y=x3+x-2的切线中,与直线4x-y=1平行的切线方程是( )
| A.4x-y=0 | B.4x-y-4=0 | C.2x-y-2=0 | D.4x-y=0或4x-y-4=0 |
函数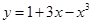 有( )
有( )
| A.极小值-1,极大值1 | B.极小值-2,极大值3 |
| C.极小值-1,极大值3 | D.极小值-2,极大值2 |
如果 为偶函数,且
为偶函数,且 导数存在,则
导数存在,则 的值为( )
的值为( )
| A.0 | B.1 | C.2 | D. |