题目内容
设抛物线y2=2px(p>0)上各点到直线3x+4y+12=0的距离的最小值为1,求p的值.
解析:由题意可知,抛物线必在直线3x+4y+12=0的上方.
则直线3x+4y+12=0上方且和它相距为1的直线方程为3x+4y+7=0.
由题意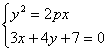 只有一解.
只有一解.
消去x得:![]() +4y+7=0.
+4y+7=0.
由Δ=16-4×![]() ×7=0,所以p=
×7=0,所以p=![]() .
.

练习册系列答案
相关题目
题目内容
设抛物线y2=2px(p>0)上各点到直线3x+4y+12=0的距离的最小值为1,求p的值.
解析:由题意可知,抛物线必在直线3x+4y+12=0的上方.
则直线3x+4y+12=0上方且和它相距为1的直线方程为3x+4y+7=0.
由题意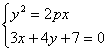 只有一解.
只有一解.
消去x得:![]() +4y+7=0.
+4y+7=0.
由Δ=16-4×![]() ×7=0,所以p=
×7=0,所以p=![]() .
.
