题目内容
(本小题满分15分)
已知动圆 过定点
过定点 ,且与直线
,且与直线 相切,椭圆
相切,椭圆 的对称轴为坐标轴,一个焦点是
的对称轴为坐标轴,一个焦点是 ,点
,点 在椭圆
在椭圆 上.
上.
(Ⅰ)求动圆圆心 的轨迹
的轨迹 的方程及其椭圆
的方程及其椭圆 的方程;
的方程;
(Ⅱ)若动直线 与轨迹
与轨迹 在
在 处的切线平行,且直线
处的切线平行,且直线 与椭圆
与椭圆 交于
交于 两点,问:是否存在着这样的直线
两点,问:是否存在着这样的直线 使得
使得 的面积等于
的面积等于 ?如果存在,请求出直线
?如果存在,请求出直线 的方程;如果不存在,请说明理由.
的方程;如果不存在,请说明理由.
【答案】
(Ⅰ)轨迹 的方程
的方程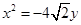 ,椭圆的方程为
,椭圆的方程为 .(Ⅱ)
.(Ⅱ) 的面积等于
的面积等于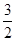 的直线
的直线 不存在.
不存在.
【解析】
试题分析:(Ⅰ)设过圆心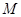 作直线直线
作直线直线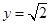 的垂线,垂足为
的垂线,垂足为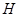 ,由题意得
,由题意得 ,即动点
,即动点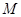 到定点
到定点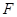 的距离与到定直线
的距离与到定直线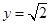 的距离相等.由抛物线的定义知,点
的距离相等.由抛物线的定义知,点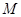 的轨迹为以
的轨迹为以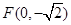 为焦点,直线
为焦点,直线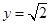 为准线的抛物线,其方程为
为准线的抛物线,其方程为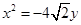 . ------3分
. ------3分
设椭圆方程为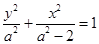 ,将点
,将点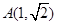 代入方程得
代入方程得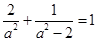 ,
,
整理得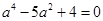 ,解得
,解得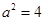 或
或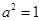 (舍去).
(舍去).
故所求椭圆的方程为 .------------------------6分
.------------------------6分
(Ⅱ)轨迹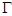 的方程为
的方程为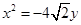 即
即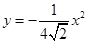 ,则
,则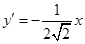 ,---------------7分
,---------------7分
所以轨迹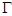 在
在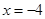 处的切线的斜率为
处的切线的斜率为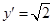 ,故直线
,故直线 的斜率为
的斜率为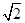 , 假设符合题意的直线方程为
, 假设符合题意的直线方程为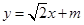 . --------8分
. --------8分
代入椭圆方程化简得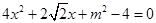 ,设
,设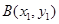 ,
,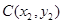 ,
,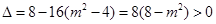 ,
,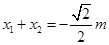 ,
,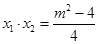 ,-----------------9分
,-----------------9分
故 ,------------------------10分
,------------------------10分
又点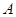 到直线
到直线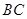 的距离是
的距离是 , --------------------11分
, --------------------11分
故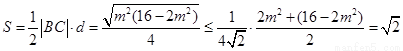 -------------------13分
-------------------13分
当且仅当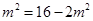 ,即
,即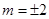 取得等号(满足
取得等号(满足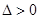 ).--------------14分
).--------------14分
此时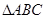 的面积等于
的面积等于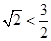 ,
,
所以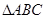 的面积等于
的面积等于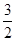 的直线
的直线 不存在.--------------15分
不存在.--------------15分
考点:椭圆的简单性质;圆的简单性质;轨迹方程的求法;直线与椭圆的综合应用。
点评:求轨迹方程的一般方法:直接法、定义法、相关点法、参数法、交轨法、向量法等。本题求轨迹方程用到的是定义法。用定义法求轨迹方程的关键是条件的转化——转化成某一已知曲线的定义条件。

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目

 的单调区间;
的单调区间; ,试分别解答以下两小题.
,试分别解答以下两小题. 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 是两个不相等的正数,且
是两个不相等的正数,且 ,求证:
,求证: .
. 、
、 分别为椭圆
分别为椭圆 :
: 的
的  :
: 的焦点,
的焦点, 是
是 。
。 :
: ,过点P的动直线
,过点P的动直线 与圆
与圆 ,
, (
( 且
且 )。求证:点Q总在某定直线上。
)。求证:点Q总在某定直线上。
 的左、右焦点分别为
的左、右焦点分别为 、
、 ,过
,过 与椭圆相交于A、B两点。
与椭圆相交于A、B两点。 ,且
,且 ,求椭圆的离心率;
,求椭圆的离心率; 求
求 的最大值和最小值。
的最大值和最小值。
 在定义域内存在区间
在定义域内存在区间 ,满足
,满足 是否为“优美函数”?若是,求出
是否为“优美函数”?若是,求出 ;若不是,说明理由;
;若不是,说明理由; 为“优美函数”,求实数
为“优美函数”,求实数 的取值范围.
的取值范围.