题目内容
过抛物线y2=4x的准线与对称轴的交点作直线,交抛物线于M、N两点,问直线的倾斜角多大时,以线段MN为直径的圆经过抛物线的焦点?
直线的倾斜角为arctan![]() 或π-?arctan
或π-?arctan![]() 时,以线段MN为直径的圆经过抛物线的?焦点.
时,以线段MN为直径的圆经过抛物线的?焦点.
解析:
抛物线y2=4x的准线与对称轴的交点为(-1,0).
设直线MN的方程为y=k(x+1).
由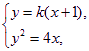
得k2x2+2(k2-2)x+k2=0.
∵直线与抛物线交于M、N两点,
∴Δ=4(k2-2)2-4k4>0,
即k2<|k2-2|,k2<1,-1<k<1.
设M(x1,y1)、N(x2,y2),抛物线焦点为F(1,0).
∵以线段MN为直径的圆经过抛物线的焦点,
∴MF⊥NF.
∴![]() =-1,
=-1,
即y1y2+x1x2-(x1+x2)+1=0.
又x1+x2=-![]() ,x1x2=1,
,x1x2=1,
y12y22=16x1x2=16且y1、y2同号,
∴![]() =-6.
=-6.
解得k2=![]() .∴k=±
.∴k=±![]() .
.
故直线的倾斜角为arctan![]() 或π-?arctan
或π-?arctan![]() 时,以线段MN为直径的圆经过抛物线的?焦点.
时,以线段MN为直径的圆经过抛物线的?焦点.

练习册系列答案
相关题目
倾斜角为
的直线过抛物线y2=4x的焦点且与抛物线交于A,B两点,则|AB|=( )
| π |
| 4 |
A、
| ||
B、8
| ||
| C、16 | ||
| D、8 |
过抛物线y2=4x的焦点F的直线交抛物线于A、B两点,点O是坐标原点,若|AF|=5,则△AOB的面积为( )
| A、5 | ||
B、
| ||
C、
| ||
D、
|