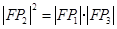题目内容
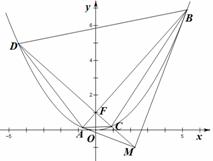 (13分)已知抛物线
(13分)已知抛物线![]() 的焦点为
的焦点为![]() ,过焦点
,过焦点![]() 且不平行于x轴的动直线
且不平行于x轴的动直线![]() 交抛物线于
交抛物线于![]() ,
,![]() 两点,抛物线在
两点,抛物线在![]() 、
、![]() 两点处的切线交于点
两点处的切线交于点![]() .
.
(Ⅰ)求证:![]() ,
,![]() ,
,![]() 三点的横坐标成等差数列;
三点的横坐标成等差数列;
(Ⅱ)设直线![]() 交该抛物线于
交该抛物线于![]() ,
,![]() 两点,求四边形
两点,求四边形![]() 面积的最小值.
面积的最小值.
(13分)
解:(Ⅰ)由已知,得![]() ,显然直线
,显然直线![]() 的斜率存在且不得0,
的斜率存在且不得0,
则可设直线![]() 的方程为
的方程为![]() (
(![]() ),
),![]() ,
,![]() ,
,
由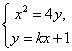 消去
消去![]() ,得
,得![]() ,显然
,显然![]() .
.
所以![]() ,
,![]() . ………………………………………………2分
. ………………………………………………2分
由![]() ,得
,得![]() ,所以
,所以![]() ,
,
所以,直线![]() 的斜率为
的斜率为![]() ,
,
所以,直线![]() 的方程为
的方程为![]() ,又
,又![]() ,
,
所以,直线![]() 的方程为
的方程为 ![]() ①。………………………………4分
①。………………………………4分
同理,直线![]() 的方程为
的方程为 ![]() ②。………………………………5分
②。………………………………5分
②-①并据![]() 得点M的横坐标
得点M的横坐标![]() ,
,
即![]() ,
,![]() ,
,![]() 三点的横坐标成等差数列。 …………………………………7分
三点的横坐标成等差数列。 …………………………………7分
(Ⅱ)由①②易得y=-1,所以点M的坐标为(2k,-1)(![]() )。
)。
所以![]() ,
,
则直线MF的方程为![]() , …………………………………………8分
, …………………………………………8分
设C(x3,y3),D(x4,y4)
由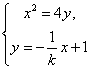 消去
消去![]() ,得
,得![]() ,显然
,显然![]() ,
,
所以![]() ,
,![]() 。 …………………………………………9分
。 …………………………………………9分
又![]()
![]() 。…………10分
。…………10分
![]()
![]() 。……………………11分
。……………………11分
因为![]() ,所以
,所以![]() ,
,
所以,![]() ,
,
当且仅当![]() 时,四边形
时,四边形![]() 面积的取到最小值
面积的取到最小值![]() 。……………………13分
。……………………13分

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
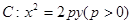 的焦点为
的焦点为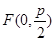 ,准线为
,准线为 ,点
,点 为抛物线C上的一点,且
为抛物线C上的一点,且 的外接圆圆心到准线的距离为
的外接圆圆心到准线的距离为 .
.
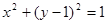 ,过点P作圆F的2条切线分别交
,过点P作圆F的2条切线分别交 轴于点
轴于点 ,求
,求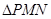 面积的最小值时
面积的最小值时 的值.
的值. 的焦点为
的焦点为 ,点
,点 ,
, 在抛物线上,且
在抛物线上,且 , 则有 ( )
, 则有 ( ) B.
B.
 D.
D.
 的焦点为
的焦点为 ,
, 过
过 轴的垂线交抛物线于
轴的垂线交抛物线于 两点.有下列四个命题:①
两点.有下列四个命题:① 必为直角三角形;②
必为直角三角形;② 必与抛物线相切;④直线
必与抛物线相切;④直线 的焦点为F,准线为
的焦点为F,准线为 ,经过F且斜率为
,经过F且斜率为 的直线与抛物线在
的直线与抛物线在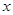 轴上方的部分相交于点A,且AK
轴上方的部分相交于点A,且AK
 的面积是( )
的面积是( ) C
C  D 8
D 8 的焦点为
的焦点为 ,点
,点 ,
, 在抛物线上,且
在抛物线上,且 ,则有( )
,则有( ) B.
B.
 D.
D.