Question

已知函数f(x)=

2x+1

+k定义域为D，且方程f（x）=x在D上有两个不等实根，则k的取值范围是（　　）

• A、-1＜k≤-

  1

  2

• B、

  1

  2

  ≤k＜1
• C、k＞-1
• D、k＜1

Answer 1

分析：根据函数f(x)=

2x+1

+k，我们可得方程f（x）=x的表达式，
（法一）我们可以根据方程的根与函数零点的对应关系，将问题转化为两个函数图象有两个交点的问题，然后分析临界直线性质，构造关于k的不等式，解不等式即可得到答案．
（法二）利用平方法去掉绝对值符号后，将问题转化为一个二次方程在定区间有两相异实根问题，构造函数，利用二次函数的性质，构造关于k的不等式，解不等式即可得到答案．

解答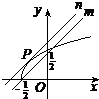：解：依题意

2x+1

=x-k在[-

1

2

，+∞)上有两个不等实根．
（方法一）问题可化为y=

2x+1

和y=x-k在[-

1

2

，+∞)上有两个不同交点、
对于临界直线m，应有-k≥

1

2

，即k≤-

1

2

．
对于临界直线n，化简方程

2x+1

=x-k，
得x²-（2k+2）x+k²-1=0，
令△=0，解得k=-1，
∴n：y=x+1，令x=0，得y=1，
∴-k＜1，即k＞-1．
综上，-1＜k≤-

1

2

．
（方法二）化简方程

2x+1

=x-k，
得x²-（2k+2）x+k²-1=0．
令g（x）=x²-（2k+2）x+k²-1，
则由根的分布可得

g(- 1 2 )≥0 k+1＞- 1 2 △＞0

，即

(k+ 1 2 )2≥0 k＞- 3 2 k＞-1

，
解得k＞-1．又

2x+1

=x-k，
∴x≥k，∴k≤-

1

2

．
综上，-1＜k≤-

1

2

．

点评：本题考查的知识点是根的存在性及根的个数判断，其中根据已知条件，构造关于k的不等式，是解答本题的关键．