题目内容
已知 为R上的连续可导函数,当
为R上的连续可导函数,当 时,
时, ,则关于
,则关于 的函数
的函数 的零点的个数为
的零点的个数为
 为R上的连续可导函数,当
为R上的连续可导函数,当 时,
时, ,则关于
,则关于 的函数
的函数 的零点的个数为
的零点的个数为 | A.1 | B.2 | C. | D. 或 或 |
C
解:
解:∵当x≠0时,f′(x)+f(x)x>0,
∴[xf′(x)+f(x)]/x>0
要求关于x的方程f(x)+1/x=0的根的个数可转化成xf(x)+1=0的根的个数
令F(x)=xf(x)+1
当x>0时,xf′(x)+f(x)>0即F′(x)>0,∴F(x)在(0,+∞)上单调递增
当x<0时,xf′(x)+f(x)<0即F′(x)<0,∴F(x)在(0,+∞)上单调递减
而y=f(x)为R上的连续可导的函数
∴xf(x)+1=0无实数根
解:∵当x≠0时,f′(x)+f(x)x>0,
∴[xf′(x)+f(x)]/x>0
要求关于x的方程f(x)+1/x=0的根的个数可转化成xf(x)+1=0的根的个数
令F(x)=xf(x)+1
当x>0时,xf′(x)+f(x)>0即F′(x)>0,∴F(x)在(0,+∞)上单调递增
当x<0时,xf′(x)+f(x)<0即F′(x)<0,∴F(x)在(0,+∞)上单调递减
而y=f(x)为R上的连续可导的函数
∴xf(x)+1=0无实数根

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
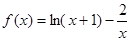 的零点所在
的零点所在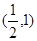
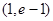
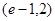
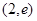
 +2(m+3)x+2m+14=0有两个不同的实根,且一个大于4,另一个小于4,求m的取值范围.
+2(m+3)x+2m+14=0有两个不同的实根,且一个大于4,另一个小于4,求m的取值范围.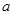 满足
满足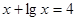 ,
,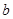 满足
满足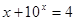 ,函数
,函数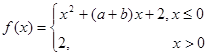 ,则关于
,则关于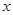 的方程
的方程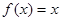 的解的个数是
的解的个数是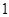
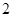
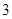
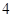
 在区间(a,b)上有零点”是“
在区间(a,b)上有零点”是“ ”的________条件
”的________条件 的零点为 ( )
的零点为 ( ) 



 的零点一定位于下列哪个区间
的零点一定位于下列哪个区间



 的实数解的个数为__________.
的实数解的个数为__________. 的解是_________
的解是_________