题目内容
从M点出发三条射线MA,MB,MC两两成60°,且分别与球O相切于A,B,C三点,若球的体积为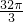 ,则OM的距离为
,则OM的距离为
- A.

- B.

- C.3
- D.4
B
分析:连接OM交平面ABC于O',由题意可得:O'A= =
= .由AO'⊥MO,OA⊥MA可得
.由AO'⊥MO,OA⊥MA可得  ,根据球的体积可得半径OA,进而求出答案.
,根据球的体积可得半径OA,进而求出答案.
解答: 解:连接OM交平面ABC于O',
解:连接OM交平面ABC于O',
由题意可得:△ABC和△MAB为正三角形,
所以O'A= =
= .
.
因为AO'⊥MO,OA⊥MA,
所以 ,
,
所以 .
.
又因为球的体积为 ,
,
所以半径OA=2,所以OM=2 .
.
故选B.
点评:本题考查球的体积和表面积、点、线、面间的距离计算,解决此类问题的方法是熟练掌握几何体的结构特征,考查计算能力和空间想象能力.
分析:连接OM交平面ABC于O',由题意可得:O'A=
 =
= .由AO'⊥MO,OA⊥MA可得
.由AO'⊥MO,OA⊥MA可得  ,根据球的体积可得半径OA,进而求出答案.
,根据球的体积可得半径OA,进而求出答案.解答:
 解:连接OM交平面ABC于O',
解:连接OM交平面ABC于O',由题意可得:△ABC和△MAB为正三角形,
所以O'A=
 =
= .
.因为AO'⊥MO,OA⊥MA,
所以
 ,
,所以
 .
.又因为球的体积为
 ,
,所以半径OA=2,所以OM=2
 .
.故选B.
点评:本题考查球的体积和表面积、点、线、面间的距离计算,解决此类问题的方法是熟练掌握几何体的结构特征,考查计算能力和空间想象能力.

练习册系列答案
相关题目
 ,则OM的距离为
,则OM的距离为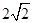 B.
B. C.3 D.4
C.3 D.4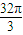 ,则OM的距离为( )
,则OM的距离为( )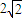
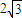
 ,则OM的距离为
,则OM的距离为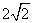 B.
B.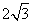 C.3 D.4
C.3 D.4