题目内容
设O点为坐标原点,曲线x2+y2+2x-6y+1=0上有两点P,Q,满足关于直线x+my+4=0对称,又满足(1)求m的值;
(2)求直线PQ的方程.
解:(1)曲线方程为(x+1)2+(y-3)2=9,表示圆心为(-1,3),半径为3的圆.
∵点P,Q在圆上且关于直线x+my+4=0对称,
∴圆心(-1,3)在直线上,代入直线方程得m=-1.
(2)∵直线PQ与直线y=x+4垂直,
∴设P(x1,y1),Q(x2,y2),PQ方程为y=-x+b.
将直线y=-x+b代入圆方程,得2x2+2(4-b)x+b2-6b+1=0.Δ=4(4-b)2-4×2×(b2-6b+1)>0,
得2-3![]() <b<2+3
<b<2+3![]() ,由韦达定理,得x1+x2=-(4-b),x1·x2=
,由韦达定理,得x1+x2=-(4-b),x1·x2=![]() ,
,
y1·y2=b2-b(x1+x2)+x1·x2=![]() +4b,∵
+4b,∵![]() ·
·![]() =0,
=0,
∴x1x2+y1y2=0,即b2-6b+1+4b=0.
解得b=1∈(2-3![]() ,2+3
,2+3![]() ).∴所求的直线方程为y=-x+1.
).∴所求的直线方程为y=-x+1.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
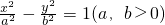 的虚轴长为2
的虚轴长为2 ,渐近线方程是y=
,渐近线方程是y=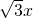 ,O为坐标原点,直线y=kx+m(k,m∈R)与双曲线C相交于A、B两点,且
,O为坐标原点,直线y=kx+m(k,m∈R)与双曲线C相交于A、B两点,且 .
. 的虚轴长为2
的虚轴长为2 ,渐近线方程是y=
,渐近线方程是y= ,O为坐标原点,直线y=kx+m(k,m∈R)与双曲线C相交于A、B两点,且
,O为坐标原点,直线y=kx+m(k,m∈R)与双曲线C相交于A、B两点,且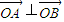 .
.