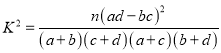题目内容
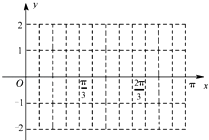
【题目】将函数f(x)=cos(ωx+φ)(ω>0,|φ|< ![]() )的图象上的每一点的纵坐标不变,横坐标缩短为原来的一半,再将图象向右平移
)的图象上的每一点的纵坐标不变,横坐标缩短为原来的一半,再将图象向右平移 ![]() 个单位长度得到函数y=sinx的图象.
个单位长度得到函数y=sinx的图象.
(1)直接写出f(x)的表达式,并求出f(x)在[0,π]上的值域;
(2)求出f(x)在[0,π]上的单调区间.
【答案】
(1)解:由题意可得,把函数y=sinx的图象向左平移 ![]() 个单位长度得到y=sin(x+
个单位长度得到y=sin(x+ ![]() )的图象,
)的图象,
再把横坐标缩短为原来的2倍,可得y=sin( ![]() x+
x+ ![]() )=cos[
)=cos[ ![]() ﹣(
﹣( ![]() x+
x+ ![]() )]=cos(
)]=cos( ![]() x﹣
x﹣ ![]() )的图象,
)的图象,
∴ ![]() .
.
∵0≤x≤π,∴ ![]() ,∴
,∴ ![]() ,∴
,∴ ![]() ,
,
当x=0时, ![]() ;当
;当 ![]() 时,f(x)=1
时,f(x)=1
(2)解:令 ![]() ,k∈Z,解得
,k∈Z,解得 ![]() ,k∈Z,
,k∈Z,
所以单调递增区间为 ![]() ,k∈Z;
,k∈Z;
同理单调递减区间为 ![]() ,k∈Z,
,k∈Z,
∵x∈[0,π],∴f(x)的单调递增区间为 ![]() ,单调递减区间为
,单调递减区间为 ![]()
【解析】(1)利用函数y=Asin(ωx+φ)的图象变换规律,正弦函数的定义域和值域,得出结论.(2)根据f(x)的解析式,以及正弦函数的单调性,得出结论.
【考点精析】解答此题的关键在于理解函数y=Asin(ωx+φ)的图象变换的相关知识,掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案【题目】将参加数学竞赛的1000名学生编号如下:0001,0002,0003,…,1000,按系统抽样的方法从中抽取一个容量为50的样本,如果在第一组抽得的编号是0015,则在第21组抽得的编号是 .
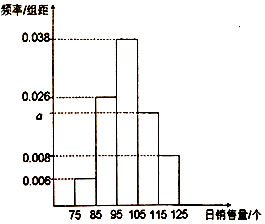
【题目】某教师调查了![]() 名高三学生购买的数学课外辅导书的数量,将统计数据制成如下表格:
名高三学生购买的数学课外辅导书的数量,将统计数据制成如下表格:
男生 | 女生 | 总计 | |
购买数学课外辅导书超过 |
|
|
|
购买数学课外辅导书不超过 |
|
|
|
总计 |
|
|
|
(Ⅰ)根据表格中的数据,是否有![]() 的把握认为购买数学课外辅导书的数量与性别相关;
的把握认为购买数学课外辅导书的数量与性别相关;
(Ⅱ)从购买数学课外辅导书不超过![]() 本的学生中,按照性别分层抽样抽取
本的学生中,按照性别分层抽样抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人询问购买原因,求恰有
人询问购买原因,求恰有![]() 名男生被抽到的概率.
名男生被抽到的概率.
附:  ,
, ![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|