题目内容
如图，长方体ABC-D'A'B'C'中，|OA|=3，|OC|=4，|OD'|=5，点P为A′C′与B′D′的交点，则点B'的坐标为（3，4，5）
（3，4，5）
；|OP|=
| ||
| 2 |
| ||
| 2 |
分析：由题意直接求出B′坐标，求出P的坐标，然后利用距离公式求解即可．
解答：解：由题意结合所给的空间直角坐标系，|OA|=3，|OC|=4，|OD′|=5，可知B′坐标（3，4，5）；
P的坐标为：（
，2，5），
所以|OP|=
=
；
故答案为：（3，4，5）；
．
P的坐标为：（
| 3 |
| 2 |
所以|OP|=
(
|
| ||
| 2 |
故答案为：（3，4，5）；
| ||
| 2 |
点评：本题是基础题，考查空间直角坐标系中的有关计算，注意点的坐标的求法，考查计算能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
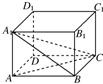6、如图在长方体ABCD-A1B1C1D1中，三棱锥A1-ABC的面是直角三角形的个数为（ ）
如图在长方体ABCD-A1B1C1D1中，三棱锥A1-ABC的面是直角三角形的个数为：
如图在长方体ABCD-A1B1C1D1中，三棱锥A1-ABC的面是直角三角形的个数为（ ）