题目内容
在△ABC中,∠BAC=60°,AB=2,AC=1,E,F为边BC的三等分点,则 =( )
=( )A.

B.

C.

D.

【答案】分析:先判定三角形形状,然后建立直角坐标系,分别求出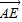 ,
,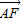 向量的坐标,代入向量数量积的运算公式,即可求出答案.
向量的坐标,代入向量数量积的运算公式,即可求出答案.
解答:解:∵在△ABC中,∠BAC=60°,AB=2,AC=1,
∴根据余弦定理可知BC=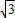
由AB=2,AC=1,BC=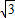 满足勾股定理可知∠BCA=90°
满足勾股定理可知∠BCA=90°
以C为坐标原点,CA、CB方向为x,y轴正方向建立坐标系
∵AC=1,BC=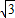 ,则C(0,0),A(1,0),B(0,
,则C(0,0),A(1,0),B(0,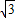 )
)
又∵E,F分别是Rt△ABC中BC上的两个三等分点,
则E(0,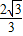 ),F(0,
),F(0,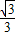 )
)
则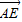 =(-1,
=(-1,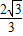 ),
),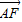 =(-1,
=(-1,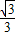 )
)
∴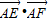 =1+
=1+ =
=
故选A.
点评:本题考查的知识点是平面向量数量积的运算,其中建立坐标系,将向量数量积的运算坐标化可以简化本题的解答过程.
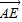 ,
,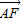 向量的坐标,代入向量数量积的运算公式,即可求出答案.
向量的坐标,代入向量数量积的运算公式,即可求出答案.解答:解:∵在△ABC中,∠BAC=60°,AB=2,AC=1,
∴根据余弦定理可知BC=
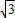
由AB=2,AC=1,BC=
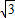 满足勾股定理可知∠BCA=90°
满足勾股定理可知∠BCA=90°以C为坐标原点,CA、CB方向为x,y轴正方向建立坐标系
∵AC=1,BC=
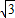 ,则C(0,0),A(1,0),B(0,
,则C(0,0),A(1,0),B(0,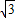 )
)又∵E,F分别是Rt△ABC中BC上的两个三等分点,
则E(0,
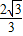 ),F(0,
),F(0,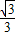 )
)则
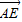 =(-1,
=(-1,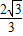 ),
),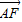 =(-1,
=(-1,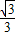 )
)∴
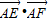 =1+
=1+ =
=
故选A.
点评:本题考查的知识点是平面向量数量积的运算,其中建立坐标系,将向量数量积的运算坐标化可以简化本题的解答过程.

练习册系列答案
相关题目
在△ABC中
等于( )
| a+b |
| a-b |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 如图,在△ABC中,
如图,在△ABC中,