题目内容
已知曲线Cn:x2-2nx+y2=0(n=1,2,…)。从点P(-1,0)向曲线Cn引斜率为kn(kn>0)的切线ln,切点为Pn(xn,yn),
(1)求数列{xn}与{yn}的通项公式;
(2)证明: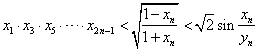 。
。
(1)求数列{xn}与{yn}的通项公式;
(2)证明:
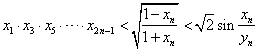 。
。 (1)解:设直线ln: ,
,
联立 得
得 ,
,
则 ,
,
∴
 ,
,
∴ ;
;
(2)证明:∵ ,
,
 ,
,
∴ ,
,
由于 ,
,
可令函数 ,
,
令 ,
,
给定区间 ,则有f′(x)<0,
,则有f′(x)<0,
则函数f(x)在 上单调递减,
上单调递减,
∴f(x)<f(0)=0,
即 在
在 恒成立,
恒成立,
又 ,
,
则有 。
。
 ,
,联立
 得
得 ,
,则
 ,
,∴

 ,
,∴
 ;
;(2)证明:∵
 ,
, ,
,∴
 ,
,由于
 ,
,可令函数
 ,
,令
 ,
,给定区间
 ,则有f′(x)<0,
,则有f′(x)<0,则函数f(x)在
 上单调递减,
上单调递减,∴f(x)<f(0)=0,
即
 在
在 恒成立,
恒成立,又
 ,
,则有
 。
。 
练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
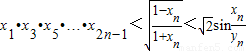 .
.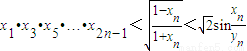 .
. .
.