题目内容
已知函数 是奇函数.
是奇函数.
(1)求实数a的值;
(2)判断函数f(x)在R上的单调性并用定义法证明;
(3)若对任意x∈R+不等式 恒成立,求实数m的范围.
恒成立,求实数m的范围.
解:(1)由题意,f(-x)=-f(x),
∴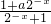 =-
=-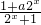
∴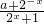 =-
=-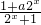
∴a=-1;
(2)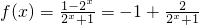 在R上为减函数,证明如下:
在R上为减函数,证明如下:
设x1<x2,则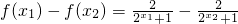 =
=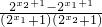
∵x1<x2,∴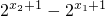 >0
>0
∴f(x1)-f(x2)>0
∴f(x1)>f(x2)
∴f(x)在R上为减函数;
(3)不等式 恒成立,等价于
恒成立,等价于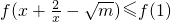
∵f(x)在R上为减函数
∴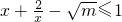
∴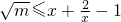
∵x>0,∴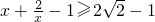
∴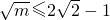
∴0≤m≤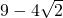 .
.
分析:(1)利用奇函数的定义,列出等式,即可求实数a的值;
(2)化简函数,求得函数的单调性,再利用定义进行证明;
(3)先化为具体不等式,再分离参数求最值,即可求实数m的范围.
点评:本题考查函数的单调性与奇偶性,考查恒成立问题,确定函数的单调性,转化为具体不等式是关键,属于中档题.
∴
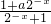 =-
=-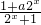
∴
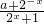 =-
=-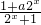
∴a=-1;
(2)
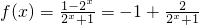 在R上为减函数,证明如下:
在R上为减函数,证明如下:设x1<x2,则
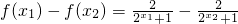 =
=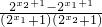
∵x1<x2,∴
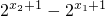 >0
>0∴f(x1)-f(x2)>0
∴f(x1)>f(x2)
∴f(x)在R上为减函数;
(3)不等式
 恒成立,等价于
恒成立,等价于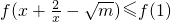
∵f(x)在R上为减函数
∴
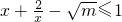
∴
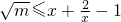
∵x>0,∴
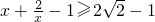
∴
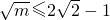
∴0≤m≤
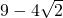 .
.分析:(1)利用奇函数的定义,列出等式,即可求实数a的值;
(2)化简函数,求得函数的单调性,再利用定义进行证明;
(3)先化为具体不等式,再分离参数求最值,即可求实数m的范围.
点评:本题考查函数的单调性与奇偶性,考查恒成立问题,确定函数的单调性,转化为具体不等式是关键,属于中档题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
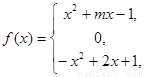
 是奇函数.
是奇函数.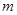 的值;
的值; 在区间
在区间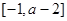 上单调递增,求实数
上单调递增,求实数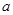 的取值范围;
的取值范围;
 是奇函数.
是奇函数.