题目内容
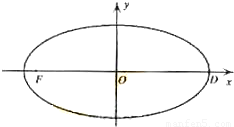 已知在平面直角坐标系xOy中的一个椭圆,它的中心在原点,左焦点为
已知在平面直角坐标系xOy中的一个椭圆,它的中心在原点,左焦点为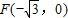 ,右顶点为D(2,0),设点
,右顶点为D(2,0),设点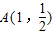 .
.(1)求该椭圆的标准方程;
(2)若P是椭圆上的动点,求线段PA中点M的轨迹方程;
(3)过原点O的直线交椭圆于点B,C,求△ABC面积的最大值.
【答案】分析:(1)由“左焦点为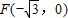 ,右顶点为D(2,0)”得到椭圆的半长轴a,半焦距c,再求得半短轴b最后由椭圆的焦点在x轴上求得方程.
,右顶点为D(2,0)”得到椭圆的半长轴a,半焦距c,再求得半短轴b最后由椭圆的焦点在x轴上求得方程.
(2)设线段PA的中点为M(x,y),点P的坐标是(x,y),由中点坐标公式,分别求得x,y,代入椭圆方程,可求得线段PA中点M的轨迹方程.
(3)分直线BC垂直于x轴时和直线BC不垂直于x轴两种情况分析,求得弦长|BC|,原点到直线的距离建立三角形面积模型,再用基本不等式求其最值.
解答:解:(1)由已知得椭圆的半长轴a=2,半焦距c=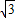 ,则半短轴b=1.
,则半短轴b=1.
又椭圆的焦点在x轴上,
∴椭圆的标准方程为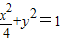
(2)设线段PA的中点为M(x,y),点P的坐标是(x,y),
由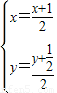 得
得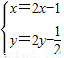
由,点P在椭圆上,得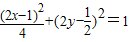 ,
,
∴线段PA中点M的轨迹方程是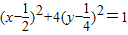 .
.
(3)当直线BC垂直于x轴时,BC=2,
因此△ABC的面积S△ABC=1.
当直线BC不垂直于x轴时,说该直线方程为y=kx,代入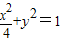 ,
,
解得B(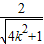 ,
,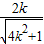 ),C(-
),C(-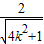 ,-
,-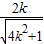 ),
),
则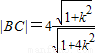 ,又点A到直线BC的距离d=
,又点A到直线BC的距离d=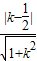 ,
,
∴△ABC的面积S△ABC=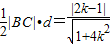
于是S△ABC=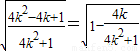
由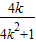 ≥-1,得S△ABC≤
≥-1,得S△ABC≤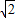 ,其中,当k=-
,其中,当k=- 时,等号成立.
时,等号成立.
∴S△ABC的最大值是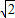 .
.
点评:本题主要考查椭圆的几何性质,直线与椭圆的位置关系,还考查了三角形面积模型的建立和解模型的能力.
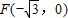 ,右顶点为D(2,0)”得到椭圆的半长轴a,半焦距c,再求得半短轴b最后由椭圆的焦点在x轴上求得方程.
,右顶点为D(2,0)”得到椭圆的半长轴a,半焦距c,再求得半短轴b最后由椭圆的焦点在x轴上求得方程.(2)设线段PA的中点为M(x,y),点P的坐标是(x,y),由中点坐标公式,分别求得x,y,代入椭圆方程,可求得线段PA中点M的轨迹方程.
(3)分直线BC垂直于x轴时和直线BC不垂直于x轴两种情况分析,求得弦长|BC|,原点到直线的距离建立三角形面积模型,再用基本不等式求其最值.
解答:解:(1)由已知得椭圆的半长轴a=2,半焦距c=
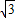 ,则半短轴b=1.
,则半短轴b=1.又椭圆的焦点在x轴上,
∴椭圆的标准方程为
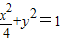
(2)设线段PA的中点为M(x,y),点P的坐标是(x,y),
由
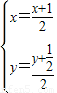 得
得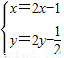
由,点P在椭圆上,得
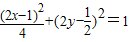 ,
,∴线段PA中点M的轨迹方程是
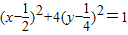 .
.(3)当直线BC垂直于x轴时,BC=2,
因此△ABC的面积S△ABC=1.
当直线BC不垂直于x轴时,说该直线方程为y=kx,代入
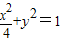 ,
,解得B(
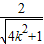 ,
,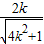 ),C(-
),C(-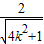 ,-
,-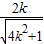 ),
),则
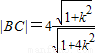 ,又点A到直线BC的距离d=
,又点A到直线BC的距离d=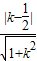 ,
,∴△ABC的面积S△ABC=
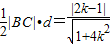
于是S△ABC=
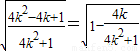
由
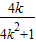 ≥-1,得S△ABC≤
≥-1,得S△ABC≤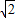 ,其中,当k=-
,其中,当k=- 时,等号成立.
时,等号成立.∴S△ABC的最大值是
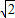 .
.点评:本题主要考查椭圆的几何性质,直线与椭圆的位置关系,还考查了三角形面积模型的建立和解模型的能力.

练习册系列答案
相关题目