Question

如图，在多面体ABCDE中，DB⊥平面ABC，AE∥DB，且△ABC是边长为2的等边三角形，AE=1，CD与平面ABDE所成角的正弦值为。
（1）在线段DC上是否存在一点F，使得EF⊥面DBC，若存在，求线段DF的长度，若不存在，说明理由；（2）求二面角D-EC-B的平面角的余弦值。

Answer 1

解：（1）取AB的中点G，连结CG，则CG⊥AB， 又DB⊥面ABC，可得DB⊥CG，所以CG⊥面ABDE， 所以，，CG=， 故CD=，， 取CD的中点为F，BC的中点为H， 因为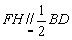，，所以AEFH为平行四边形， 得EF∥AH， 平面BCD， ∴EF⊥面DBC， 所以，存在点F，当F为CD的中点，DF=时，使得EF⊥面DBC。
（2）如图建立空间直角坐标系，则、、、 ， 从而，，， 设为平面BCE的法向量， 则可以取， 设为平面CDE的法向量， 则取， 因此，， 故二面角D-EC-B的余弦值为。