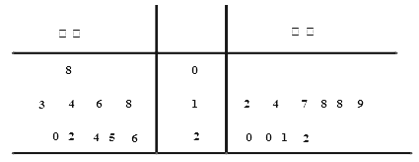
题目内容
【题目】已知集合![]() ,
,![]() ,
,![]()
![]() ,令
,令![]() 表示集合
表示集合![]() 所含元素的个数.
所含元素的个数.
(1)写出![]() 的值;
的值;
(2)当![]() 时,写出
时,写出![]() 的表达式,并用数学归纳法证明.
的表达式,并用数学归纳法证明.
【答案】(1)13
(2)
【解析】
试题(1)根据题意按![]() 分类计数:
分类计数:![]()
![]()
![]() 共13个(2)由(1)知
共13个(2)由(1)知![]()
![]()
![]() ,所以当
,所以当![]() 时,
时,![]() 的表达式要按
的表达式要按![]() 除的余数进行分类,最后不难利用数学归纳法进行证明
除的余数进行分类,最后不难利用数学归纳法进行证明
试题解析:(1)![]() .
.
(2)当![]() 时,
时, (
(![]() ).
).
下面用数学归纳法证明:
①当![]() 时,
时,![]() ,结论成立;
,结论成立;
②假设![]() (
(![]() )时结论成立,那么
)时结论成立,那么![]() 时,
时,![]() 在
在![]() 的基础上新增加的元素在
的基础上新增加的元素在![]() ,
,![]() ,
,![]() 中产生,分以下情形讨论:
中产生,分以下情形讨论:
1)若![]() ,则
,则![]() ,此时有
,此时有![]()
![]() ,结论成立;
,结论成立;
2)若![]() ,则
,则![]() ,此时有
,此时有![]()
![]() ,结论成立;
,结论成立;
3)若![]() ,则
,则![]() ,此时有
,此时有![]()
![]() ,结论成立;
,结论成立;
4)若![]() ,则
,则![]() ,此时有
,此时有![]()
![]() ,结论成立;
,结论成立;
5)若![]() ,则
,则![]() ,此时有
,此时有![]()
![]() ,结论成立;
,结论成立;
6)若![]() ,则
,则![]() ,此时有
,此时有![]()
![]() ,结论成立.
,结论成立.
综上所述,结论对满足![]() 的自然数
的自然数![]() 均成立.
均成立.

【题目】“绿水青山就是金山银山”,“建设美丽中国”已成为新时代中国特色社会主义生态文明建设的重要内容,某班在一次研学旅行活动中,为了解某苗圃基地的柏树幼苗生长情况,在这些树苗中随机抽取了120株测量高度(单位:![]() ),经统计,树苗的高度均在区间
),经统计,树苗的高度均在区间![]() 内,将其按
内,将其按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6组,制成如图所示的频率分布直方图.据当地柏树苗生长规律,高度不低于
分成6组,制成如图所示的频率分布直方图.据当地柏树苗生长规律,高度不低于![]() 的为优质树苗.
的为优质树苗.

(1)求图中![]() 的值;
的值;
(2)已知所抽取的这120株树苗来自于![]() ,
,![]() 两个试验区,部分数据如下列联表:
两个试验区,部分数据如下列联表:
|
| 合计 | |
优质树苗 | 20 | ||
非优质树苗 | 60 | ||
合计 |
将列联表补充完整,并判断是否有99.9%的把握认为优质树苗与![]() ,
,![]() 两个试验区有关系,并说明理由;
两个试验区有关系,并说明理由;
(3)通过用分层抽样方法从![]() 试验区被选中的树苗中抽取5株,若从这5株树苗中随机抽取2株,求优质树苗和非优质树苗各有1株的概率.
试验区被选中的树苗中抽取5株,若从这5株树苗中随机抽取2株,求优质树苗和非优质树苗各有1株的概率.
附:参考公式与参考数据:
其中![]()
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
【题目】有一种密码,明文是由三个字符组成,密码是由明文对应的五个数字组成,编码规则如下表:明文由表中每一排取一个字符组成,且第一排取的字符放在第一位,第二排取的字符放在第二位,第三排取的字符放在第三位,对应的密码由明文对应的数字按相同的次序排成一排组成.
| 明文字符 | A | B | C | D |
密码字符 | 11 | 12 | 13 | 14 | |
| 明文字符 | E | F | G | H |
密码字符 | 21 | 22 | 23 | 24 | |
| 明文字符 | M | N | P | Q |
密码字符 | 1 | 2 | 3 | 4 |
设随机变量![]() 表示密码中不同数字的个数.
表示密码中不同数字的个数.
(Ⅰ)求![]() 的分布列和它的数学期望.
的分布列和它的数学期望.