题目内容
已知函数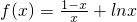
(1)求f(x)在[ ,2]上的最大值和最小值;(参考数据:ln2≈0.7)
,2]上的最大值和最小值;(参考数据:ln2≈0.7)
(2)求证:ln
 ;
;
(3)求证:对大于1的任意正整数n,都有 lnn +
+ +
+ +…+
+…+ .
.
(1)解:求导函数,可得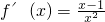
∴x∈[ ,1]时,f′(x)<0,函数单调递减,x∈(1,2]时,f′(x)>0,函数单调递增
,1]时,f′(x)<0,函数单调递减,x∈(1,2]时,f′(x)>0,函数单调递增
∴f(x)在[ ,2]上有唯一极小值点,且为最小值点,最小值为f(1)=0
,2]上有唯一极小值点,且为最小值点,最小值为f(1)=0
∵ ,
,
∴ =
=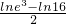 >0
>0
∴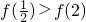
∴f(x)在[ ,2]上的最大值为1-ln2;
,2]上的最大值为1-ln2;
(2)证明:当a=1时,f(x)=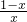 +lnx,f′(x)=
+lnx,f′(x)= ,
,
故f(x)在[1,+∞)上为增函数.
当n>1时,令x= ,则x>1,故f(x)>f(1)=0
,则x>1,故f(x)>f(1)=0
∴f( )=
)=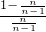 +ln
+ln =-
=- +ln
+ln >0,即ln
>0,即ln >
> ;
;
(3)证明:由(2)知,ln >
> ,ln
,ln >
> ,…,ln
,…,ln >
>
∴ln +ln
+ln +…+ln
+…+ln >
> +
+ +…+
+…+
∴lnn> +
+ +…+
+…+
即对大于1的任意正整数n,都有lnn> +
+ +…+
+…+ .
.
分析:(1)求导函数,确定函数的单调性,比较端点的函数值,即可求得结论;
(2)先判断函数f(x)的单调性,令x= 代入函数f(x)根据单调性,即可得到不等式ln
代入函数f(x)根据单调性,即可得到不等式ln >
> ,
,
(3)由(2)令n=1,2,…代入可证.
点评:本题主要考查函数的单调性与其导函数的正负之间的关系,考查函数的最值,考查不等式的证明,考查学生分析解决问题的能力,属于中档题.
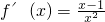
∴x∈[
 ,1]时,f′(x)<0,函数单调递减,x∈(1,2]时,f′(x)>0,函数单调递增
,1]时,f′(x)<0,函数单调递减,x∈(1,2]时,f′(x)>0,函数单调递增∴f(x)在[
 ,2]上有唯一极小值点,且为最小值点,最小值为f(1)=0
,2]上有唯一极小值点,且为最小值点,最小值为f(1)=0∵
 ,
,∴
 =
=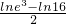 >0
>0∴
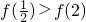
∴f(x)在[
 ,2]上的最大值为1-ln2;
,2]上的最大值为1-ln2;(2)证明:当a=1时,f(x)=
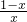 +lnx,f′(x)=
+lnx,f′(x)= ,
,故f(x)在[1,+∞)上为增函数.
当n>1时,令x=
 ,则x>1,故f(x)>f(1)=0
,则x>1,故f(x)>f(1)=0∴f(
 )=
)=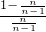 +ln
+ln =-
=- +ln
+ln >0,即ln
>0,即ln >
> ;
;(3)证明:由(2)知,ln
 >
> ,ln
,ln >
> ,…,ln
,…,ln >
>
∴ln
 +ln
+ln +…+ln
+…+ln >
> +
+ +…+
+…+
∴lnn>
 +
+ +…+
+…+
即对大于1的任意正整数n,都有lnn>
 +
+ +…+
+…+ .
.分析:(1)求导函数,确定函数的单调性,比较端点的函数值,即可求得结论;
(2)先判断函数f(x)的单调性,令x=
 代入函数f(x)根据单调性,即可得到不等式ln
代入函数f(x)根据单调性,即可得到不等式ln >
> ,
,(3)由(2)令n=1,2,…代入可证.
点评:本题主要考查函数的单调性与其导函数的正负之间的关系,考查函数的最值,考查不等式的证明,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目


 上恒成立,求实数m的取值范围.
上恒成立,求实数m的取值范围.

