题目内容
椭圆 (2a>3b)的焦点F1、F2在x轴上,点P为椭圆上一点且∠F1PF2不大于120°,则它的离心率的取值范围是
(2a>3b)的焦点F1、F2在x轴上,点P为椭圆上一点且∠F1PF2不大于120°,则它的离心率的取值范围是
- A.
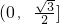
- B.

- C.

- D.

B
分析:由题意推出P位于短轴端点时,∠F1PF2最大,通过 与
与 ∠F1PF2的关系,求出e的范围,求出2a>3b中e的范围,即可得到离心率的范围.
∠F1PF2的关系,求出e的范围,求出2a>3b中e的范围,即可得到离心率的范围.
解答:因为椭圆中P位于短轴端点时,∠F1PF2最大,
由题意可知tan ∠F1PF2=
∠F1PF2=
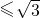 ,
,
所以 ,即
,即 ,
,
解得e≤ .
.
又因为2a>3b,
∴4a2>9b2=9(a2-c2),
解得e> .
.
所以 e∈ .
.
故选B.
点评:本题是基础题,考查椭圆的基本性质,注意P在短轴端点时,∠F1PF2最大,以及3a>2b,是解题的关键,考查计算能力.
分析:由题意推出P位于短轴端点时,∠F1PF2最大,通过
 与
与 ∠F1PF2的关系,求出e的范围,求出2a>3b中e的范围,即可得到离心率的范围.
∠F1PF2的关系,求出e的范围,求出2a>3b中e的范围,即可得到离心率的范围.解答:因为椭圆中P位于短轴端点时,∠F1PF2最大,
由题意可知tan
 ∠F1PF2=
∠F1PF2=
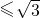 ,
,所以
 ,即
,即 ,
,解得e≤
 .
.又因为2a>3b,
∴4a2>9b2=9(a2-c2),
解得e>
 .
.所以 e∈
 .
.故选B.
点评:本题是基础题,考查椭圆的基本性质,注意P在短轴端点时,∠F1PF2最大,以及3a>2b,是解题的关键,考查计算能力.

练习册系列答案
相关题目
 (2a>3b)的焦点F1、F2在x轴上,点P为椭圆上一点且∠F1PF2不大于120°,则它的离心率的取值范围是( )
(2a>3b)的焦点F1、F2在x轴上,点P为椭圆上一点且∠F1PF2不大于120°,则它的离心率的取值范围是( )


