题目内容
如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=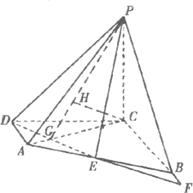
(Ⅰ)求证:平面PDE⊥平面PAC;
(Ⅱ)求直线PC与平面PDE所成的角;
(Ⅲ)求点B到平面PDE的距离.
解法一:(Ⅰ)设AC与DE交点为G,延长DE交CB延长线于点F,则△DAE≌△FBE,
∴BF=AD=1,∴CF=4,
∴tan∠F=![]()
又tan∠ACD=![]() ,
,
∴∠F=∠ACD,
又∵∠ACD+∠ACF=90°,
∴∠F+∠ACF=90°,
∴∠CGF=90°,
∴AC⊥DE,
又∵PC⊥底面ABCD,∴PC⊥DE,∴DE⊥平面PAC,
∵DE![]() 平面PDE,∴平面PDE⊥平面PAC.
平面PDE,∴平面PDE⊥平面PAC.
(Ⅱ)连结PG,过点C作CH⊥PG于H点,则由(Ι)知平面PDE上平面PAC,且PG是交线,根据面面垂直的性质,得CH⊥平面PDE,从而∠CPH即∠CPG为直线PC与平面PDE所成的角.

在Rt△DCA中,CG=![]()
在Rt△PCG中,tan∠CPG=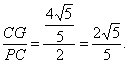
所以有∠CPG=arctan ![]() .
.
即直线PC与平面PDE所成的角为arctan![]() .
.
(Ⅲ)由于BF=![]() CF,所以可知点B到平面PDE的距离等于点C到平面PDE的距离的
CF,所以可知点B到平面PDE的距离等于点C到平面PDE的距离的![]() ,即
,即![]() CH.
CH.
在Rt△PCG中,CH=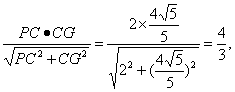
从而点D到平面PDE的距离等于![]() .
.
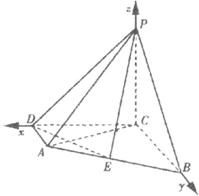
解法二:如图所示,以点C为坐标原点,直线CD、CB、CP分别为x、y、z轴,建立空间直角坐标系C-xyz,
则相关点的坐标为C(0,0,0),A(2,1,0),B(0,3,0),
(Ⅰ)由于![]() =(-1,2,0),
=(-1,2,0),![]() =(2,1,0),
=(2,1,0),![]() =(0,0,2),
=(0,0,2),
所以![]() ·
·![]() =(-1,2,0)·(2,1,0)=0,
=(-1,2,0)·(2,1,0)=0,
![]() ·
·![]() =(-1,2,0)·(0,0,2)=0.
=(-1,2,0)·(0,0,2)=0.
所以DE⊥CA,DE⊥CP.
而CP∩CA=C,所以DE⊥平面PAC.
∵DE![]() 平面PDE,∴平面PDE⊥平面PAC.
平面PDE,∴平面PDE⊥平面PAC.
(Ⅱ)设n=(x,y,z)是平面PDE的一个法向量,则n·![]() =n·
=n·![]() =0,
=0,
由于![]() =(-1,2,0),
=(-1,2,0), ![]() =(1,2,-2),所以有
=(1,2,-2),所以有
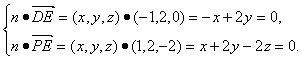
令x=2,则y=1,z=2,即n=(2,1,2),
再设直线PC与平面PDE所成的角为α
而![]() =(0,0,-2),所以
=(0,0,-2),所以
sinα=|cos〈n,![]() 〉|=
〉|=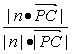
=![]() ,
,
∴α=arcsin![]() ,
,
因此直线PC与平面PDE所成的角为arcsin![]() .
.
(Ⅲ)由(Ⅱ)知n=(2,1,2)是平面PDE的一个法向量,而![]() (1,-1,0),所以点B到平面PDE的距离为
(1,-1,0),所以点B到平面PDE的距离为![]()

 如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.
如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.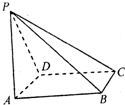 如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4,
如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4,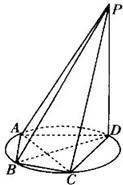 如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD.
如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD. (2012•烟台一模)如图所示,四棱锥P-ABCD中,ABCD为正方形,PA⊥AD,E,F,G分别是线段PA,PD,CD的中点.
(2012•烟台一模)如图所示,四棱锥P-ABCD中,ABCD为正方形,PA⊥AD,E,F,G分别是线段PA,PD,CD的中点. 如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.
如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.