题目内容
已知数列{an}是等比数列,Sn为其前n项和.(1)若S4,S10,S7成等差数列,证明a1,a7,a4也成等差数列;
(2)设
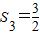 ,
,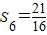 ,bn=λan-n2,若数列{bn}是单调递减数列,求实数λ的取值范围.
,bn=λan-n2,若数列{bn}是单调递减数列,求实数λ的取值范围.
【答案】分析:(1)设数列{an}的公比为q,根据等差中项的性质可知2S10=S4+S7,代入等比数列求和公式整理得1+q3=2q6.进而根据等比数列的通项公式可推断a1+a4=2a7.进而证明原式.
(2)把等比数列的求和公式代入S3和S6,两式相除即可求得q,把q代入S3求得a1,进而可得数列{an}的通项公式,根据数列{bn}是单调递减数列可知bn+1<bn,把bn=λan-n2代入不等式,进而根据当n是奇数时,当n=1时取最大值;n是偶数时,当n=2时取最大值,进而得到λ的范围.
解答:解:(1)证明:设数列{an}的公比为q,
因为S4,S10,S7成等差数列,所以q≠1,且2S10=S4+S7.
所以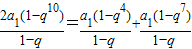 ,
,
因为1-q≠0,所以1+q3=2q6.
所以a1+a1q3=2a1q6,即a1+a4=2a7.
所以a1,a7,a4也成等差数列.
(2)因为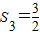 ,
,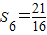 ,
,
所以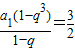 ,①
,①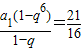 ,②
,②
由②÷①,得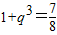 ,所以
,所以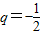 ,代入①,得a1=2.
,代入①,得a1=2.
所以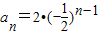 ,
,
又因为bn=λan-n2,所以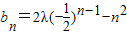 ,
,
由题意可知对任意n∈N*,数列{bn}单调递减,
所以bn+1<bn,即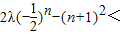
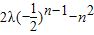 ,
,
即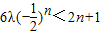 对任意n∈N*恒成立,
对任意n∈N*恒成立,
当n是奇数时,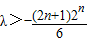 ,当n=1时,
,当n=1时,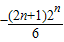 取得最大值-1,
取得最大值-1,
所以λ>-1;
当n是偶数时,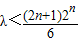 ,当n=2时,
,当n=2时,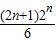 取得最小值
取得最小值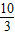 ,
,
所以λ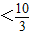 .
.
综上可知,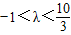 ,即实数λ的取值范围是
,即实数λ的取值范围是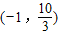 .
.
点评:本题主要考查等比数列的性质,考查了学生根据已知条件,分析和解决问题的能力.
(2)把等比数列的求和公式代入S3和S6,两式相除即可求得q,把q代入S3求得a1,进而可得数列{an}的通项公式,根据数列{bn}是单调递减数列可知bn+1<bn,把bn=λan-n2代入不等式,进而根据当n是奇数时,当n=1时取最大值;n是偶数时,当n=2时取最大值,进而得到λ的范围.
解答:解:(1)证明:设数列{an}的公比为q,
因为S4,S10,S7成等差数列,所以q≠1,且2S10=S4+S7.
所以
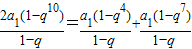 ,
,因为1-q≠0,所以1+q3=2q6.
所以a1+a1q3=2a1q6,即a1+a4=2a7.
所以a1,a7,a4也成等差数列.
(2)因为
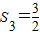 ,
,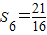 ,
,所以
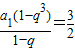 ,①
,①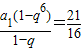 ,②
,②由②÷①,得
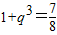 ,所以
,所以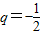 ,代入①,得a1=2.
,代入①,得a1=2.所以
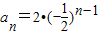 ,
,又因为bn=λan-n2,所以
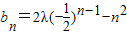 ,
,由题意可知对任意n∈N*,数列{bn}单调递减,
所以bn+1<bn,即
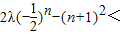
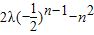 ,
,即
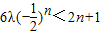 对任意n∈N*恒成立,
对任意n∈N*恒成立,当n是奇数时,
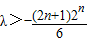 ,当n=1时,
,当n=1时,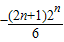 取得最大值-1,
取得最大值-1,所以λ>-1;
当n是偶数时,
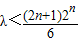 ,当n=2时,
,当n=2时,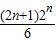 取得最小值
取得最小值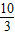 ,
,所以λ
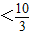 .
.综上可知,
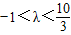 ,即实数λ的取值范围是
,即实数λ的取值范围是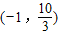 .
.点评:本题主要考查等比数列的性质,考查了学生根据已知条件,分析和解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目