Question

设点F₁（-c，0），F₂（c，0）分别是椭圆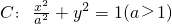的左、右焦点，P为椭圆C上任意一点，且最小值为0．
（1）求椭圆C的方程；
（2）设定点D（m，0），已知过点F₂且与坐标轴不垂直的直线l与椭圆交于A、B两点，满足|AD|=|BD|，求m的取值范围．

Answer 1

解：（1）设P（x，y），则，，
∴，
由题意得，1-c²=0?c=1?a²=2，
∴椭圆C的方程为．
（2）由（1）得F（1，0），设l的方程为y=k（x-1），
代入，得（2k²+1）x²-4k²x+2k²-2=0，
设A（x₁，y₁），B（x₂，y₂），则，∴，
设AB的中点为M，则，
∵|AD|=|BD|，∴DM⊥AB，即k_CM•k_AB=-1，∴
∵直线l与坐标轴不垂直，∴．
∴．
分析：（1）设出点P的坐标，利用数量积得到表达式，根据其取得最小值的条件即可得出c，进而得出椭圆的方程；
（2）利用点斜式得到直线l的方程，与椭圆方程联立，再利用根与系数的关系及垂直平分线的性质即可求出m的范围．
点评：熟练掌握椭圆的定义与性质、向量的数量积、线段的垂直平分线的性质、直线与圆锥曲线相交问题的解题模式、一元二次方程根与系数的关系是解题的关键．