题目内容
对于函数 与
与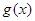 和区间D,如果存在
和区间D,如果存在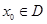 ,使
,使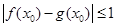 ,则称
,则称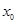 是函数
是函数 与
与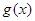 在区间D上的“友好点”.现给出两个函数:
在区间D上的“友好点”.现给出两个函数:
①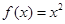 ,
,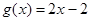 ;
;
②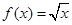 ,
, ;
;
③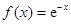 ,
,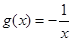 ;
;
④
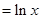 ,
, ,
,
则在区间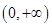 上的存在唯一“友好点”的是( )
上的存在唯一“友好点”的是( )
| A.①② | B.③④ | C.②③ | D.①④ |
D
解析试题分析:对于① ,所以,存在唯一“友好点”
,所以,存在唯一“友好点” 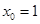 ;
;
对于②, ,不符合
,不符合 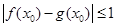 ;
;
对于③,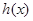 =
=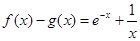 ,
,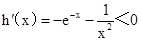 ,函数
,函数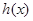 在(0,+∞)上是单调减函数,当
在(0,+∞)上是单调减函数,当 时,
时, ,所以,存在
,所以,存在 ,使
,使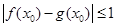 成立,但“友好点”不唯一;
成立,但“友好点”不唯一;
对于④
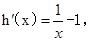 令
令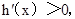 得
得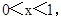
令 ,得
,得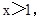 所以,
所以, 时,函数取得极大值,且为最大值,最大值为
时,函数取得极大值,且为最大值,最大值为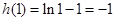 ,所以,存在存在唯一“友好点”
,所以,存在存在唯一“友好点”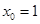 ;故在区间
;故在区间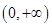 上的存在唯一“友好点”的是①④,选D.
上的存在唯一“友好点”的是①④,选D.
考点:新定义问题,配方法、导数法求函数的值域.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
函数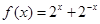 的图象关于 对称. ( )
的图象关于 对称. ( )
| A.坐标原点 | B.直线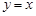 | C. 轴 轴 | D.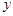 轴 轴 |
设函数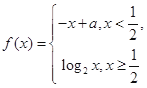 的最小值为
的最小值为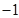 ,则实数
,则实数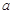 的取值范围是( )
的取值范围是( )
A.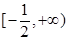 | B.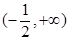 | C.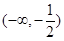 | D.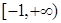 |
已知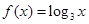 ,则
,则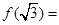 ( )
( )
A.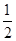 | B. | C.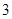 | D.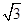 |
设 ,则函数
,则函数 ( )
( )
A.在 上单调递减,在 上单调递减,在 上单调递增 上单调递增 |
B.在 上单调递增,在 上单调递增,在 上单调递减 上单调递减 |
C.在 上单调递增,在 上单调递增,在 上单调递增 上单调递增 |
D.在 上单调递减,在 上单调递减,在 上单调递减 上单调递减 |
若 ,则下列结论正确的是( )
,则下列结论正确的是( )
A.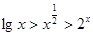 | B.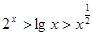 |
C.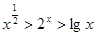 | D.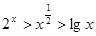 |
函数 由
由 确定,则方程
确定,则方程 的实数解有( )
的实数解有( )
| A.0个 | B.1个 | C.2个 | D.3个 |
函数y= ln(1-x)的定义域为( )
ln(1-x)的定义域为( )
| A.(0,1) | B.[0,1) | C.(0,1] | D.[0,1) |
若 ,则
,则 的大小顺序是
的大小顺序是
A. | B. | C. | D.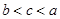 |