题目内容
若90°＜θ＜180°，曲线x2+y2sinθ=1表示（ ）A．焦点在x轴上的双曲线
B．焦点在y轴上的双曲线
C．焦点在x轴上的椭圆
D．焦点在y轴上的椭圆
【答案】分析：求出sinθ值的范围，把曲线化为标准形式x2 +
=1，判断曲线的形状．
解答：解：若90°＜θ＜180°，则 0＜sinθ＜1，曲线x2+y2sinθ=1 即 x2 +
=1，
表示焦点在y轴上的椭圆，
故选 D．
点评：本题考查椭圆的标准方程的特征，正弦函数的值域，把曲线化为标准形式x2 +
=1，是解题的关键．
=1，判断曲线的形状．解答：解：若90°＜θ＜180°，则 0＜sinθ＜1，曲线x2+y2sinθ=1 即 x2 +
=1，表示焦点在y轴上的椭圆，
故选 D．
点评：本题考查椭圆的标准方程的特征，正弦函数的值域，把曲线化为标准形式x2 +
=1，是解题的关键． 
练习册系列答案
相关题目
+
=1（a＞b＞0）的右焦点为F（4m，0）（M＞0，m为常数），离心率等于0.8，过焦点F、倾斜角为θ的直线l交椭圆C于M、N两点．
+
=
，求实数m；
+
的值是否与θ的大小无关，并证明你的结论．
、
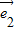满足
，
，且
、
的夹角为60°，设向量
与向量
的夹角为θ（t∈R）．
