题目内容
已知函数f(x)=2sinxcosx+2cos2x(x∈R).
(Ⅰ)求f(x)的最小正周期,并求f(x)的最小值.
(Ⅱ)令 ,若g(x)<a-2对于
,若g(x)<a-2对于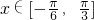 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
解:(Ⅰ)∵f(x)=2sinxcosx+2cos2x=sin2x+cos2x+1= sin(2x+
sin(2x+ )+1,
)+1,
∴f(x)的最小正周期 T= =π.由于-1≤sin(2x+
=π.由于-1≤sin(2x+ )≤1,∴1-
)≤1,∴1- ≤f(x)≤
≤f(x)≤ +1,
+1,
故f(x)的最小值是 1- .
.
(Ⅱ)由题意可得 =
= sin[2(x+
sin[2(x+ )+
)+ ]+1-1=
]+1-1= cos2x,
cos2x,
∵- ≤x≤
≤x≤ ,∴-
,∴- ≤2x≤
≤2x≤ ,故当x=0时,
,故当x=0时, cos2x 有最大值为
cos2x 有最大值为 ,
,
故 <a-2,∴a>2+
<a-2,∴a>2+ ,
,
故实数a的取值范围是( 2+ ,+∞).
,+∞).
分析:(Ⅰ)化简f(x)的解析式为 sin(2x+
sin(2x+ )+1,故f(x)的最小正周期 T=
)+1,故f(x)的最小正周期 T= ,根据正弦函数的值域求出f(x)的最小值.
,根据正弦函数的值域求出f(x)的最小值.
(Ⅱ)由题意求得g(x)= cos2x,根据x的范围求得 2x的范围,由此求得g(x)=
cos2x,根据x的范围求得 2x的范围,由此求得g(x)= cos2x 的最大值
cos2x 的最大值 ,
,
根据题意可得 <a-2,从而求得实数a的取值范围.
<a-2,从而求得实数a的取值范围.
点评:本题考查三角函数的恒等变换,三角函数的周期性以及三角函数的最值,函数的恒成立问题,求出g(x)的解析式是解题的关键.
 sin(2x+
sin(2x+ )+1,
)+1,∴f(x)的最小正周期 T=
 =π.由于-1≤sin(2x+
=π.由于-1≤sin(2x+ )≤1,∴1-
)≤1,∴1- ≤f(x)≤
≤f(x)≤ +1,
+1,故f(x)的最小值是 1-
 .
.(Ⅱ)由题意可得
 =
= sin[2(x+
sin[2(x+ )+
)+ ]+1-1=
]+1-1= cos2x,
cos2x,∵-
 ≤x≤
≤x≤ ,∴-
,∴- ≤2x≤
≤2x≤ ,故当x=0时,
,故当x=0时, cos2x 有最大值为
cos2x 有最大值为 ,
,故
 <a-2,∴a>2+
<a-2,∴a>2+ ,
,故实数a的取值范围是( 2+
 ,+∞).
,+∞).分析:(Ⅰ)化简f(x)的解析式为
 sin(2x+
sin(2x+ )+1,故f(x)的最小正周期 T=
)+1,故f(x)的最小正周期 T= ,根据正弦函数的值域求出f(x)的最小值.
,根据正弦函数的值域求出f(x)的最小值.(Ⅱ)由题意求得g(x)=
 cos2x,根据x的范围求得 2x的范围,由此求得g(x)=
cos2x,根据x的范围求得 2x的范围,由此求得g(x)= cos2x 的最大值
cos2x 的最大值 ,
,根据题意可得
 <a-2,从而求得实数a的取值范围.
<a-2,从而求得实数a的取值范围.点评:本题考查三角函数的恒等变换,三角函数的周期性以及三角函数的最值,函数的恒成立问题,求出g(x)的解析式是解题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目