题目内容
已知a1=0,an+1=can+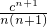 ,c≠0,n∈N*.
,c≠0,n∈N*.
(I )求数列{an}的通项:
(II)若对任意,n∈N*,an+1>an恒成立,求c的取值范围.
解:(Ⅰ)∵an+1=can+ ,∴
,∴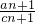 =
= +
+ ,
,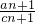 -
- =
= -
- .
.
∴ =
=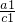 +(
+( -
-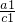 )+(
)+(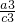 -
- )+…+(
)+…+( -
-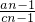 )=0+1-
)=0+1- +
+ -
- +…+
+…+ -
- =1-
=1- ,
,
∴an= cn.(6分)
cn.(6分)
(Ⅱ)an+1>an即 cn+1>
cn+1> cn.
cn.
当c<0时,上面不等式显然不恒成立;
当c>0时,上面不等式等价于c>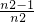 =1-
=1-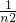 .(9分)
.(9分)
1-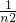 是n的增函数,
是n的增函数, (1-
(1-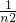 )=1,∴c≥1.
)=1,∴c≥1.
综上,c的取值范围是c≥1.(12分)
分析:(Ⅰ)由an+1=can+ ,知
,知 =
=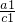 +(
+( -
-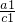 )+(
)+(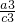 -
- )+…+(
)+…+( -
-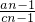 )=0+1-
)=0+1- +
+ -
- +…+
+…+ -
- =1-
=1- ,由此能求出数列{an}的通项.
,由此能求出数列{an}的通项.
(Ⅱ)an+1>an即 cn+1>
cn+1> cn.当c<0时,上面不等式显然不恒成立;当c>0时,上面不等式等价于c>
cn.当c<0时,上面不等式显然不恒成立;当c>0时,上面不等式等价于c>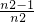 =1-
=1-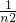 ,由此能求出c的取值范围.
,由此能求出c的取值范围.
点评:本题考查利用累加法求解函数的通项公式和借助极限知识求解参数的取值范围,解题时要注意合理地进行等价转化.
 ,∴
,∴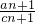 =
= +
+ ,
,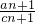 -
- =
= -
- .
.∴
 =
=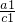 +(
+( -
-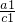 )+(
)+(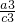 -
- )+…+(
)+…+( -
-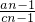 )=0+1-
)=0+1- +
+ -
- +…+
+…+ -
- =1-
=1- ,
,∴an=
 cn.(6分)
cn.(6分)(Ⅱ)an+1>an即
 cn+1>
cn+1> cn.
cn.当c<0时,上面不等式显然不恒成立;
当c>0时,上面不等式等价于c>
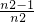 =1-
=1-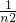 .(9分)
.(9分)1-
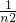 是n的增函数,
是n的增函数, (1-
(1-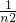 )=1,∴c≥1.
)=1,∴c≥1.综上,c的取值范围是c≥1.(12分)
分析:(Ⅰ)由an+1=can+
 ,知
,知 =
=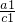 +(
+( -
-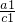 )+(
)+(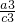 -
- )+…+(
)+…+( -
-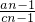 )=0+1-
)=0+1- +
+ -
- +…+
+…+ -
- =1-
=1- ,由此能求出数列{an}的通项.
,由此能求出数列{an}的通项.(Ⅱ)an+1>an即
 cn+1>
cn+1> cn.当c<0时,上面不等式显然不恒成立;当c>0时,上面不等式等价于c>
cn.当c<0时,上面不等式显然不恒成立;当c>0时,上面不等式等价于c>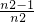 =1-
=1-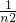 ,由此能求出c的取值范围.
,由此能求出c的取值范围.点评:本题考查利用累加法求解函数的通项公式和借助极限知识求解参数的取值范围,解题时要注意合理地进行等价转化.

练习册系列答案
相关题目