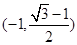题目内容
函数 的值域是
的值域是
- A.[-2,+∞)
- B.(-∞,-2]
- C.(0,1)
- D.(-∞,2]
B
分析:题目给出的是复合函数,要求函数的值域,先求真数的范围,注意真数要大于0,然后运用对数函数在底数为 时是减函数求值域.
时是减函数求值域.
解答:令t=x2-2x+5,由x2-2x+5=(x-1)2+4≥4,知原函数的定义域为R,t≥4,
则 ,所以原函数的值域为(-∞,-2].
,所以原函数的值域为(-∞,-2].
故答案为B.
点评:本题考查了复合函数值域的求法,解答的关键是求出内层函数的值域,求解时一定要保证对数式的真数大于0,属易错题.
分析:题目给出的是复合函数,要求函数的值域,先求真数的范围,注意真数要大于0,然后运用对数函数在底数为
 时是减函数求值域.
时是减函数求值域.解答:令t=x2-2x+5,由x2-2x+5=(x-1)2+4≥4,知原函数的定义域为R,t≥4,
则
 ,所以原函数的值域为(-∞,-2].
,所以原函数的值域为(-∞,-2].故答案为B.
点评:本题考查了复合函数值域的求法,解答的关键是求出内层函数的值域,求解时一定要保证对数式的真数大于0,属易错题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,则函数
,则函数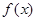 的值域是( ).
的值域是( ).  B.
B.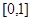 C.
C.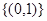 D.
D.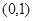
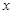 是一个三角形的最小内角,则函数
是一个三角形的最小内角,则函数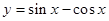 的值域是( )
的值域是( ) B.
B.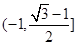 C.
C.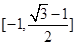 D.
D.