题目内容
已知函数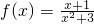
(1)求f(x)的极值;
(2)若对任意x1,x2∈[-3,2],有f(x1)-f(x2)≤m成立,求实数m的最小值.
解:(1)函数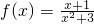 ,则f′(x)=
,则f′(x)=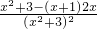 =
=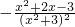
令f′(x)=0解得x=-3,或x=1,且当x∈(-∞,-3)时,f′(x)<0,故f(x)为减函数;
当x∈(-3,1)时,f′(x)>0,故f(x)为增函数;
当x∈(1,+∞)时,f′(x)<0,故f(x)为减函数.
故函数在x=-3处取到极小值f(-3)= ,在x=1处取到极大值f(1)=
,在x=1处取到极大值f(1)=
(2)由(1)可知函数f(x)在[-3,1]上为增函数,在[1,2]上为减函数,
故函数在[-3,2]上有唯一的极大值即是最大值为f(1)= ,
,
又f(-3)= ,f(2)=
,f(2)= ,故最小值为
,故最小值为
f(x1)-f(x2)≤m成立,只需m≥[f(x1)-f(x2)]max=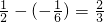
故实数m的最小值为
分析:(1)求导数,令其等于0判两侧的单调性得可得极值;
(2)由(1)可判区间[-3,2]的单调性,进而可得极值,可求最值,把恒成立问题转化为最值问题,函数在所研究区间上的函数差值的最大值即为最大值与最小值的差.
点评:本题为函数极值与最值的求解,正确运用极值与最值的定义是解决问题的关键,属中档题.
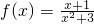 ,则f′(x)=
,则f′(x)=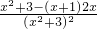 =
=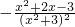
令f′(x)=0解得x=-3,或x=1,且当x∈(-∞,-3)时,f′(x)<0,故f(x)为减函数;
当x∈(-3,1)时,f′(x)>0,故f(x)为增函数;
当x∈(1,+∞)时,f′(x)<0,故f(x)为减函数.
故函数在x=-3处取到极小值f(-3)=
 ,在x=1处取到极大值f(1)=
,在x=1处取到极大值f(1)=
(2)由(1)可知函数f(x)在[-3,1]上为增函数,在[1,2]上为减函数,
故函数在[-3,2]上有唯一的极大值即是最大值为f(1)=
 ,
,又f(-3)=
 ,f(2)=
,f(2)= ,故最小值为
,故最小值为
f(x1)-f(x2)≤m成立,只需m≥[f(x1)-f(x2)]max=
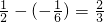
故实数m的最小值为

分析:(1)求导数,令其等于0判两侧的单调性得可得极值;
(2)由(1)可判区间[-3,2]的单调性,进而可得极值,可求最值,把恒成立问题转化为最值问题,函数在所研究区间上的函数差值的最大值即为最大值与最小值的差.
点评:本题为函数极值与最值的求解,正确运用极值与最值的定义是解决问题的关键,属中档题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目


 上恒成立,求实数m的取值范围.
上恒成立,求实数m的取值范围.

