题目内容
等差数列{an}的公差d不为零，首项a1=1，a2是a1和a5的等比中项．
（1）求数列{an}的通项公式及前n项和Sn
（2）证明数列
为等比数列；
（3）求数列
的前n项和Tn．
（1）解：由题意知，∵a2是a1和a5的等比中项
∴（a1+d）2=a1（a1+4d），
即a12+2a1d+d2=a12++4a1d，
∴d=2a1=2．
∴an=1+（n-1）×2=2n-1，
（2）证明：∵
∴数列为等比数列；
（3）解：
∴数列的前n项和Tn=
=
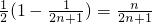
分析：（1）根据第二项是第一第五项的比例中项求出公差，从而可求数列{an}的通项公式及前n项和Sn．
（2）利用等比数列的定义可证；
（3）对通项进行裂项，再进行求和即可．
点评：本题考查的重点是数列的通项与求和，解题的关键是利用等差数列与等比数列的定义，利用裂项法求和．
∴（a1+d）2=a1（a1+4d），
即a12+2a1d+d2=a12++4a1d，
∴d=2a1=2．
∴an=1+（n-1）×2=2n-1，
（2）证明：∵
∴数列
为等比数列；（3）解：
∴数列
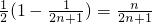
的前n项和Tn==分析：（1）根据第二项是第一第五项的比例中项求出公差，从而可求数列{an}的通项公式及前n项和Sn．
（2）利用等比数列的定义可证；
（3）对通项进行裂项，再进行求和即可．
点评：本题考查的重点是数列的通项与求和，解题的关键是利用等差数列与等比数列的定义，利用裂项法求和．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目