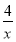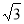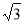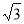题目内容
在三棱锥 中,
中, 且
且 .
.

(Ⅰ)求证: ;
;
(Ⅱ)求三棱锥的体积 .
.
(Ⅰ)证明过程详见试题解析;(Ⅱ) .
.
【解析】
试题分析:(Ⅰ)由线线垂直得到线面垂直,再根据直线所在的平面得到线线垂直;(Ⅱ)根据三棱锥的体积公式 求之.
求之.
试题解析:(Ⅰ)证明:因为 ,所以
,所以 .
.
又因为 ,所以
,所以 平面
平面 ,所以
,所以 .
.
又 ,所以
,所以 .所以
.所以 平面
平面 .故
.故 .
.
(Ⅱ)在 中,
中, ,所以
,所以 .
.
又在 中,
中, ,所以
,所以 .
.
又因为 平面
平面 ,所以
,所以 .
.
考点:(Ⅰ)线面垂直的性质定理;(Ⅱ)三棱锥的体积公式.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目