题目内容
在等差数列 中,
中, ,其前
,其前 项和为
项和为 ,等比数列
,等比数列 的各项均为正数,
的各项均为正数, ,公比为
,公比为 ,且
,且 ,
,
 .
.
(Ⅰ)求 与
与 ;(Ⅱ)设数列
;(Ⅱ)设数列 满足
满足 ,求
,求 的前
的前 项和
项和
【答案】
Ⅰ)设 的公差为
的公差为 ,
,
因为 所以
所以 ,即
,即 ---2分
---2分

 或
或 (舍),
(舍),
 .---4分
.---4分
故 ,
, . ----------6分
. ----------6分
(Ⅱ) =
= ,------8分
,------8分


 . ---10分
. ---10分

 .
.
【解析】(1)根据 ,
,  可建立关于公差d,公比q的两个方程,求出d,q,进而可确定
可建立关于公差d,公比q的两个方程,求出d,q,进而可确定 与
与 ;
;
(2)在(1)的基础上,求出Sn,然后在求 的前n项和时,采用裂项求和的方法即可
的前n项和时,采用裂项求和的方法即可

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,
中, ,其前n项和为
,其前n项和为 ,若
,若 ,则
,则 的值等于 .
的值等于 .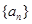 中,
中,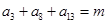 ,其前n项
,其前n项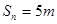 ,则n=
,则n=  中,
中, ,其前n项
,其前n项 ,则n=
,则n=  中,
中, 则其前11项的和
则其前11项的和 ( )
( ) D.128
D.128 中,
中, 则其前11项的和
则其前11项的和 ( )
( )  B.
B. C.
C. D.
D.