题目内容
设x,y满足约束条件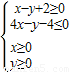 ,若目标函数z=ax+by(a>0,b>0)的最大值为6,则
,若目标函数z=ax+by(a>0,b>0)的最大值为6,则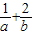 的最小值为 .
的最小值为 .
【答案】分析:画出不等式组表示的平面区域,利用目标函数z=ax+by(a>0,b>0)的最大值为6,可得2a+4b=6,即1=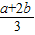 ,利用“1”的代换,根据基本不等式,可求最小值.
,利用“1”的代换,根据基本不等式,可求最小值.
解答: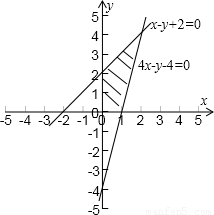 解:画出不等式组表示的平面区域,
解:画出不等式组表示的平面区域,
可知当直线z=ax+by,经过点(2,4)时,z取最大值,所以2a+4b=6,即1=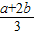 ,
,
∴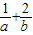 =
=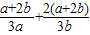 =
= +
+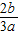 +
+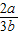 ≥3,故
≥3,故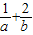 的最小值为3.
的最小值为3.
故答案为3
点评:本题考查线性规划知识,考查基本不等式的运用,求得a,b的关系是关键.
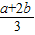 ,利用“1”的代换,根据基本不等式,可求最小值.
,利用“1”的代换,根据基本不等式,可求最小值.解答:
 解:画出不等式组表示的平面区域,
解:画出不等式组表示的平面区域,可知当直线z=ax+by,经过点(2,4)时,z取最大值,所以2a+4b=6,即1=
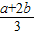 ,
,∴
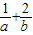 =
=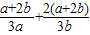 =
= +
+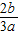 +
+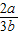 ≥3,故
≥3,故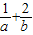 的最小值为3.
的最小值为3.故答案为3
点评:本题考查线性规划知识,考查基本不等式的运用,求得a,b的关系是关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目