题目内容
已知椭圆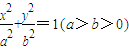 的两焦点F1、F2和短轴的两端点B1、B2正好是一正方形的四个顶点,且焦点到椭圆上一点的最近距离为
的两焦点F1、F2和短轴的两端点B1、B2正好是一正方形的四个顶点,且焦点到椭圆上一点的最近距离为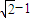 .
.(1)求椭圆的标准方程;
(2)设P是椭圆上任一点,MN是圆C:x2+(y-2)2=1的任一条直径,求
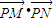 的最大值.
的最大值.
【答案】分析:(1)由题意知 可求得a,c和b的值,进而椭圆的方程可得.
可求得a,c和b的值,进而椭圆的方程可得.
(2)根据 ═
═ 从而只需求出
从而只需求出 的最大值,设P(x,y)代入椭圆方程可得x和y,的关系式,再根据C点坐标求得
的最大值,设P(x,y)代入椭圆方程可得x和y,的关系式,再根据C点坐标求得 关于y的关系式,进而根据的范围求得
关于y的关系式,进而根据的范围求得 的范围,进而求得
的范围,进而求得 的最大值.
的最大值.
解答:解:(1)由题意知 ,
,
故椭圆的标准方程为 .
.
(2) =
=
从而只需求出 的最大值
的最大值
设P(x,y),
则有 ,
,
即有x2=2-2y2,又C(0,2),
所以 ,
,
而y∈[-1,1],
所以y=-1时, 最大值为9,
最大值为9,
故 的最大值为8.
的最大值为8.
点评:本题主要考查了椭圆的性质.属基础题.
 可求得a,c和b的值,进而椭圆的方程可得.
可求得a,c和b的值,进而椭圆的方程可得.(2)根据
 ═
═ 从而只需求出
从而只需求出 的最大值,设P(x,y)代入椭圆方程可得x和y,的关系式,再根据C点坐标求得
的最大值,设P(x,y)代入椭圆方程可得x和y,的关系式,再根据C点坐标求得 关于y的关系式,进而根据的范围求得
关于y的关系式,进而根据的范围求得 的范围,进而求得
的范围,进而求得 的最大值.
的最大值.解答:解:(1)由题意知
 ,
,故椭圆的标准方程为
 .
.(2)
 =
=
从而只需求出
 的最大值
的最大值设P(x,y),
则有
 ,
,即有x2=2-2y2,又C(0,2),
所以
 ,
,而y∈[-1,1],
所以y=-1时,
 最大值为9,
最大值为9,故
 的最大值为8.
的最大值为8.点评:本题主要考查了椭圆的性质.属基础题.

练习册系列答案
相关题目
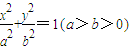 的两焦点F1、F2和短轴的两端点B1、B2正好是一正方形的四个顶点,且焦点到椭圆上一点的最近距离为
的两焦点F1、F2和短轴的两端点B1、B2正好是一正方形的四个顶点,且焦点到椭圆上一点的最近距离为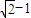 .
.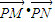 的最大值.
的最大值.