题目内容
如图，l是平面α的斜线，斜足是O，A是l上任意一点，AB是平面α的垂线，B是垂足，设OD是平面α内与OB不同的一条直线，AC垂直于OD于C，若直线l与平面α所成的角θ=45°，∠BOC=45°，求∠AOC的大小．
解：∵AB⊥α平面，AC⊥OD 根据三垂线定理可得，OC⊥BC
在Rt△OABcos∠AOB=
=
，Rt△OCB中
=，Rt△AOC
∴cos∠AOB•cos∠BOC=
=cos∠AOC
∴
∴∠AOC=60°
分析：由已知 根据三垂线定理可得，OC⊥BC，根据三角函数可得cos∠AOB•cos∠BOC=cos∠AOC，结合已知可求．
点评：本题主要考查了三余弦定理的应用，解决本题的关键是要熟练应用三垂线定理找出已知角之间的余弦关系．
在Rt△OABcos∠AOB=
=，Rt△OCB中=，Rt△AOC∴cos∠AOB•cos∠BOC=
=cos∠AOC∴
∴∠AOC=60°
分析：由已知 根据三垂线定理可得，OC⊥BC，根据三角函数可得cos∠AOB•cos∠BOC=cos∠AOC，结合已知可求．
点评：本题主要考查了三余弦定理的应用，解决本题的关键是要熟练应用三垂线定理找出已知角之间的余弦关系．
练习册系列答案
相关题目
15、如图是表示以AB=4，BC=3的矩形ABCD为底面的长方体被一平面斜截所得的几何体，其中四边形EFGH为截面．已知AE=5，BF=8，CG=12．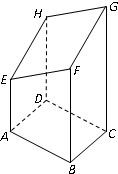
如图是表示以AB=4，BC=3的矩形ABCD为底面的长方体被一平面斜截所得的几何体，其中四边形EFGH为截面．已知AE=5，BF=8，CG=12．