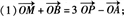题目内容
已知A、B、M三点不共线,对于平面ABM外的任一点O,确定在下列各条件下,点P是否与A、B、M一定共面?(1)![]() ;
;
(2)![]()
解法一:(1)原式可变形为
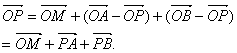
由共面向量定理的推论知点P与A、B、M共面.
(2)原式可变形为
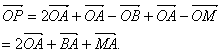
由共面向量定理的推论可得
点P位于平面ABM内的充要条件可写成
![]()
而此题推得![]()
∴点P与A、B、M不共面.
解法二:
(1)原式可变形为![]()
∵3+(-1)+(-1)=1,∴点B与P、A、M共面,
即点P与A、B、M共面.
(2)![]()
∵4+(-1)+(-1)=2≠1,
∴点P与A、B、M不共面.
绿色通道:
判断点P是否位于平面MAB内,关键是看向量![]() 能否用向量
能否用向量![]() 、
、![]() 表示(或看向量
表示(或看向量![]() 是否能写成
是否能写成![]() 的形式).当
的形式).当![]() 能用
能用![]() 、
、![]() 表示时,P位于平面MAB内;当
表示时,P位于平面MAB内;当![]() 不能用
不能用![]() 、
、![]() 表示时,点P不在平面MAB内.当
表示时,点P不在平面MAB内.当![]() =x
=x![]() +y
+y![]() +z
+z![]() 时,点P与M、A、B共面的充要条件是x+y+z=1.
时,点P与M、A、B共面的充要条件是x+y+z=1.

练习册系列答案
相关题目
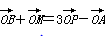 ,则点P与A、B、M( )
,则点P与A、B、M( )