��Ŀ����
����С������12�֣�Ϊ���˽�ij���1000��ѧ���İ��׳ɼ�����������ȡ������ѧ���İ��׳ɼ����ɼ�ȫ������13����18��֮�䣬���ɼ������·�ʽ�ֳ����飺��һ��[13��14�����ڶ���[14��15��;����;������[17��18].���������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ����֪ͼ�д����ҵ�ǰ3�����Ƶ��֮��Ϊ3��8��19���ҵڶ����Ƶ��Ϊ8.
����Ƶ�ʵ������ʣ�����Ƹ����ѧ���а��׳ɼ���[16��17���ڵ�������
����������������ȡ�˶��ٸ�ѧ���İ��׳ɼ���
�������ӵ�һ�����������ȡ�������ɼ������������ɼ��IJ�ľ���ֵ����1��ĸ���.
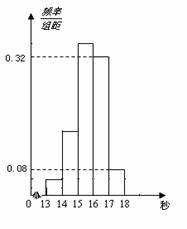
��:�����׳ɼ���[16,17)�ڵ�Ƶ��Ϊ0.32![]() 1=0.32 ,��0.32
1=0.32 ,��0.32![]() 1000=320
1000=320
����Ƹ����ѧ���а��׳ɼ���[16,17)�ڵ�����Ϊ320��. 2��
������ͼ�д�����ǰ3�����Ƶ�ʷֱ�Ϊ3x��8x ��19x �����⣬��
3x+8x+19x+0.32![]() 1+0.08
1+0.08![]() 1=1 ����x=0.02
1=1 ����x=0.02
������������ȡ��n ��ѧ���İ��׳ɼ�����![]() ��n=50
��n=50
������������ȡ��50��ѧ���İ��׳ɼ�. 6��
�����׳ɼ��ڵ�һ���ѧ������3![]() 0.02
0.02![]() 1
1![]() 50=3�������ǵijɼ�Ϊa��b��c
50=3�������ǵijɼ�Ϊa��b��c
���׳ɼ��ڵ������ѧ������0.08![]() 1
1![]() 50= 4�������ǵijɼ�Ϊm��n��p��q
50= 4�������ǵijɼ�Ϊm��n��p��q
��ӵ�һ�����������ȡ�������ɼ������Ļ����¼���
{a,b},{a,c},{a,m},{a,n},{a,p},{a,q},{b,c},{b,m},{b,n},{b,p},{b,q},{c,m},{c,n},{c,p},{c,q},
{m,n},{m,p},{m,q},{n,p},{n,q},{p,q}����21��
��������ɼ��IJ�ľ���ֵ����1���������Ļ����¼���{a,m},{a,n},{a,p},{a,q}��{b,m},{b,n},{b,p},{b,q}��{c,m},{c,n},{c,p},{c,q}����12���� ����P=![]() .
.
