题目内容
函数 ,?m,n∈[0,5](m<n),使f(x)在[m,n]上的值域为[m,n],则这样的实数对(m,n)共有
,?m,n∈[0,5](m<n),使f(x)在[m,n]上的值域为[m,n],则这样的实数对(m,n)共有
- A.1个
- B.2个
- C.3个
- D.4个
D
分析:先画出函数的图象,结合函数的图象分①0≤m<n<3,②3≤m<n≤5,③0≤m<3<n<5三种情况,判断函数的表达式及在对应区间上的单调性可求.
解答:先画出函数的图象,如图所示,由题意可得m≠0
①当0≤m<n<3时,f(x)= 在区间[m,n]单调递增,则
在区间[m,n]单调递增,则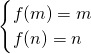 ?
? ?
?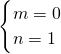
②当3≤m<n≤5,f(x)=10-2x在[m,n]单调递减,则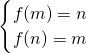 ?
? ?m=n(舍)
?m=n(舍)
③当0≤m<3<n<5时,可知函数的最大值为f(3)=4=n,从而可得函数的定义域及值域为[m,4],而f(4)=2
(i)当m=2时,定义域[2,4],f(2)= >f(4)=2,故值域为[2,4]符合题意
>f(4)=2,故值域为[2,4]符合题意
(ii)当m<2时, =m可得m=1,n=4,符合题意
=m可得m=1,n=4,符合题意
(iii)当m=0时,定义域[0,4],f(3)=4>f(4)=2,故值域为[0,4]符合题意
综上可得符合题意的有(0,1),(0,4),(1,4),(2,4)
故选D.

点评:本题主要考查了分段函数的值域的求解,解题中如能借助于函数的图象,可以简化运算,要注意数形结合及分类讨论思想在解题中的运用.
分析:先画出函数的图象,结合函数的图象分①0≤m<n<3,②3≤m<n≤5,③0≤m<3<n<5三种情况,判断函数的表达式及在对应区间上的单调性可求.
解答:先画出函数的图象,如图所示,由题意可得m≠0
①当0≤m<n<3时,f(x)=
 在区间[m,n]单调递增,则
在区间[m,n]单调递增,则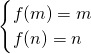 ?
? ?
?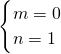
②当3≤m<n≤5,f(x)=10-2x在[m,n]单调递减,则
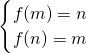 ?
? ?m=n(舍)
?m=n(舍)③当0≤m<3<n<5时,可知函数的最大值为f(3)=4=n,从而可得函数的定义域及值域为[m,4],而f(4)=2
(i)当m=2时,定义域[2,4],f(2)=
 >f(4)=2,故值域为[2,4]符合题意
>f(4)=2,故值域为[2,4]符合题意(ii)当m<2时,
 =m可得m=1,n=4,符合题意
=m可得m=1,n=4,符合题意(iii)当m=0时,定义域[0,4],f(3)=4>f(4)=2,故值域为[0,4]符合题意
综上可得符合题意的有(0,1),(0,4),(1,4),(2,4)
故选D.

点评:本题主要考查了分段函数的值域的求解,解题中如能借助于函数的图象,可以简化运算,要注意数形结合及分类讨论思想在解题中的运用.

练习册系列答案
相关题目
 ,?m,n∈[0,5](m<n),使f(x)在[m,n]上的值域为[m,n],则这样的实数对(m,n)共有( )
,?m,n∈[0,5](m<n),使f(x)在[m,n]上的值域为[m,n],则这样的实数对(m,n)共有( ) ,?m,n∈[0,5](m<n),使f(x)在[m,n]上的值域为[m,n],则这样的实数对(m,n)共有( )
,?m,n∈[0,5](m<n),使f(x)在[m,n]上的值域为[m,n],则这样的实数对(m,n)共有( ) ,?m,n∈[0,5](m<n),使f(x)在[m,n]上的值域为[m,n],则这样的实数对(m,n)共有( )
,?m,n∈[0,5](m<n),使f(x)在[m,n]上的值域为[m,n],则这样的实数对(m,n)共有( ) ,?m,n∈[0,5](m<n),使f(x)在[m,n]上的值域为[m,n],则这样的实数对(m,n)共有( )
,?m,n∈[0,5](m<n),使f(x)在[m,n]上的值域为[m,n],则这样的实数对(m,n)共有( )